题目内容
10.已知A(3,2),B(-4,1),C(0,-1),点Q线段AB上的点,则直线CQ的斜率取值范围是$(-∞,-\frac{1}{2}]∪[1,+∞)$.分析 kCA=1,kCB=$-\frac{1}{2}$.根据点Q线段AB上的点,即可得出直线CQ的斜率取值范围.
解答 解:kCA=$\frac{-1-2}{0-3}$=1,kCB=$\frac{-1-1}{0-(-4)}$=$-\frac{1}{2}$.
∵点Q线段AB上的点,
则直线CQ的斜率取值范围是:$(-∞,-\frac{1}{2}]∪[1,+∞)$.
故答案为:$(-∞,-\frac{1}{2}]∪[1,+∞)$.
点评 本题考查了直线的斜率计算公式及其应用,考查了推理能力与计算能力,属于中档题.

练习册系列答案
 天天向上口算本系列答案
天天向上口算本系列答案
相关题目
20.已知实数x,y满足约束条件$\left\{\begin{array}{l}{x-y+1≥0}\\{4x+3y-12≤0}\\{y-2≥0}\end{array}\right.$,则z=$\frac{3x-y+2}{x+1}$的最大值为( )
| A. | $\frac{9}{5}$ | B. | $\frac{3}{2}$ | C. | $\frac{25}{16}$ | D. | $\frac{9}{4}$ |
2.点P(-1,2)到直线3x-4y+12=0的距离为( )
| A. | 5 | B. | $\frac{1}{5}$ | C. | 1 | D. | 2 |
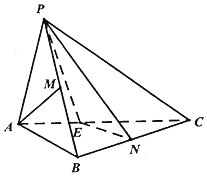 如图,三棱锥P-ABC中,BC⊥平面PAB,PA=PB=AB=6,BC=9,点M,N分别为PB,BC的中点.
如图,三棱锥P-ABC中,BC⊥平面PAB,PA=PB=AB=6,BC=9,点M,N分别为PB,BC的中点.