题目内容
12.在区间(1,2)内随机取个实数a,则直线y=2x,直线x=a与x轴围成的面积大于$\frac{16}{9}$的概率是( )| A. | $\frac{2}{3}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{2}$ | D. | $\frac{3}{4}$ |
分析 求出直线y=2x,直线x=a与x轴围成的面积大于$\frac{16}{9}$的等价条件,利用几何概型的概率公式即可得到结论.用几何概型的概率公式即可得到结论.
解答 解:当x=a时,y=2a,即A(a,2a),B(a,0),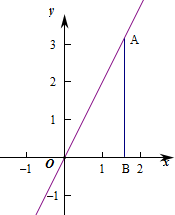
则△ABO的面积S=$\frac{1}{2}$×a×2a=a2,
若直线y=2x,直线x=a与x轴围成的面积大于$\frac{16}{9}$,
即a2>$\frac{16}{9}$,解得a>$\frac{4}{3}$,
∵1<a<2,
∴$\frac{4}{3}$<a<2,
则对应的概率P=$\frac{2-\frac{4}{3}}{2-1}$=$\frac{2}{3}$,
故选:A
点评 本题主要考查几何概型的概率的计算,根据条件求出a的取值范围是解决本题的关键.

练习册系列答案
相关题目
3.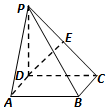 在底面是正方形的四棱锥P-ABCD中,已知PD⊥底面ABCD,且PD=CD,E为PC的中点,则异面直线PA与DE所成的角是( )
在底面是正方形的四棱锥P-ABCD中,已知PD⊥底面ABCD,且PD=CD,E为PC的中点,则异面直线PA与DE所成的角是( )
 在底面是正方形的四棱锥P-ABCD中,已知PD⊥底面ABCD,且PD=CD,E为PC的中点,则异面直线PA与DE所成的角是( )
在底面是正方形的四棱锥P-ABCD中,已知PD⊥底面ABCD,且PD=CD,E为PC的中点,则异面直线PA与DE所成的角是( )| A. | 90° | B. | 60° | C. | 45° | D. | 30° |
20.已知实数x,y满足约束条件$\left\{\begin{array}{l}{x-y+1≥0}\\{4x+3y-12≤0}\\{y-2≥0}\end{array}\right.$,则z=$\frac{3x-y+2}{x+1}$的最大值为( )
| A. | $\frac{9}{5}$ | B. | $\frac{3}{2}$ | C. | $\frac{25}{16}$ | D. | $\frac{9}{4}$ |
4.已知命题p:$\frac{1}{x-1}<1$,q:x2-(a+1)x+a>0,若p是q的充分不必要条件,则实数a的取值范围是( )
| A. | (-∞,2) | B. | [1,2] | C. | (1,2] | D. | [1,2) |
2.点P(-1,2)到直线3x-4y+12=0的距离为( )
| A. | 5 | B. | $\frac{1}{5}$ | C. | 1 | D. | 2 |



