题目内容
 已知函数f(x)=
已知函数f(x)=| 1 |
| 3 |
(Ⅰ)求实数a的值;
(Ⅱ)求f(x)在区间[-1,3]上的最大值和最小值.
考点:导数在最大值、最小值问题中的应用
专题:导数的综合应用
分析:(1)由函数极值的定义得f'(2)=0,利用导数法求得即可;
(2)利用导数判断函数的单调性并由函数的增减性求得函数的最值.
(2)利用导数判断函数的单调性并由函数的增减性求得函数的最值.
解答:
(本小题满分11分)
解:(Ⅰ)f'(x)=x2-2ax.…(2分)∵x=2是函数f(x)的一个极小值点,∴f'(2)=0.
即4-4a=0,解得a=1.…(4分)
经检验,当a=1时,x=2是函数f(x)的一个极小值点.∴实数a的值为1.…(5分)
(Ⅱ)由(Ⅰ)知,f(x)=
x3-x2+4.f'(x)=x2-2x=x(x-2).
令f'(x)=0,得x=0或x=2.…(6分)
当x在[-1,3]上变化时,f'(x),f(x)的变化情况如下:
…(9分)
当x=-1或x=2时,f(x)有最小值
;
当x=0或x=3时,f(x)有最大值4.…(11分)
解:(Ⅰ)f'(x)=x2-2ax.…(2分)∵x=2是函数f(x)的一个极小值点,∴f'(2)=0.
即4-4a=0,解得a=1.…(4分)
经检验,当a=1时,x=2是函数f(x)的一个极小值点.∴实数a的值为1.…(5分)
(Ⅱ)由(Ⅰ)知,f(x)=
| 1 |
| 3 |
令f'(x)=0,得x=0或x=2.…(6分)
当x在[-1,3]上变化时,f'(x),f(x)的变化情况如下:
| x | -1 | (-1,0) | 0 | (0,2) | 2 | (2,3) | 3 | ||||
| f'(x) | + | 0 | - | 0 | + | ||||||
| f(x) |
|
↗ | 4 | ↘ |
|
↗ | 4 |
当x=-1或x=2时,f(x)有最小值
| 8 |
| 3 |
当x=0或x=3时,f(x)有最大值4.…(11分)
点评:本题主要考查利用导数研究函数的单调性、极值、最值等知识,属常规题目,中档题.

练习册系列答案
相关题目
圆(x+2)2+(y+1)2=4关于x轴对称的圆的方程为( )
| A、(x-2)2+(y+1)2=4 |
| B、(x+2)2+(y-1)2=4 |
| C、(x-2)2+(y-1)2=4 |
| D、(x+2)2+(y+1)2=4 |
已知f(x)=
,则
的值是( )
| 1 |
| x |
| lim |
| △x→0 |
| -f(2+△x)+f(2) |
| △x |
A、
| ||
| B、2 | ||
C、-
| ||
| D、-2 |
已知α是第四象限的角,且sinα•cosα=-
,则sinα-cosα=( )
| 12 |
| 25 |
A、-
| ||
B、
| ||
C、
| ||
D、-
|
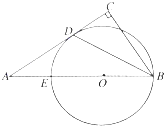 如图,在Rt△ABC中,∠C=90°,E为AB上一点,以BE为直径作圆O与AC相切于点D.若AB:BC=2:1,CD=
如图,在Rt△ABC中,∠C=90°,E为AB上一点,以BE为直径作圆O与AC相切于点D.若AB:BC=2:1,CD=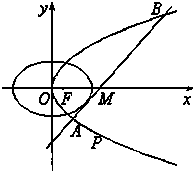 已知椭圆C1和抛物线C2有公共焦点F(1,0),C1的中心和C2的顶点都在坐标原点,过点M(4,0)的直线l与抛物线C2分别相交于A,B两点.
已知椭圆C1和抛物线C2有公共焦点F(1,0),C1的中心和C2的顶点都在坐标原点,过点M(4,0)的直线l与抛物线C2分别相交于A,B两点.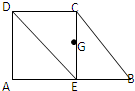 如图所示,已知直角梯形ABCD,AD⊥AB,AB=2AD=2CD,过点C作CE⊥AB于E,G为CE的中点,建立适当的坐标系,用向量的坐标表示法证明:
如图所示,已知直角梯形ABCD,AD⊥AB,AB=2AD=2CD,过点C作CE⊥AB于E,G为CE的中点,建立适当的坐标系,用向量的坐标表示法证明: