Question

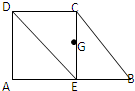如图所示，已知直角梯形ABCD，AD⊥AB，AB=2AD=2CD，过点C作CE⊥AB于E，G为CE的中点，建立适当的坐标系，用向量的坐标表示法证明：
（1）DE∥BC；
（2）D，G，B三点共线．

Answer 1

考点：平行向量与共线向量

专题：平面向量及应用

分析：（1）建立如图所示的坐标系，利用向量的坐标运算和共线定理即可得出；
（2）利用中点坐标公式和向量共线定理即可得出．

解答： 解：（1）如图所示，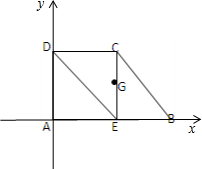
取|AB|=2，
∵直角梯形ABCD，AD⊥AB，AB=2AD=2CD，过点C作CE⊥AB于E，
∴B（2，0），E（1，0），D（0，1），C（1，1）．
∴

DE

=（1，0）-（0，1）=（1，-1），

CB

=（2，0）-（1，1）=（1，-1），
∴

DE

=

CB

，
∵点C不在DE上，
∴DE∥CB．
（2）∵G为CE的中点，∴G(1，

1

2

)．
∴

DG

=(1，

1

2

)-(0，1)=(1，-

1

2

)，

GB

=(2，0)-(1，

1

2

)=(1，-

1

2

)，
∴

DG

=

GB

．
∴D，G，B三点共线．

点评：本题考查了向量的坐标运算和共线定理、中点坐标公式，属于基础题．