题目内容
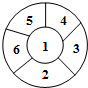如图，有一个圆环型花圃，要在花圃的6个部分栽种4种不同颜色的花，每部分栽种1种，且相邻部分栽种不同颜色的花，则不同的栽种方法有考点：排列、组合及简单计数问题
专题：应用题,排列组合
分析：先栽种1，有四种选择，再栽种2，有3种选择，第三步栽种3，有2种选择，第四步栽种4时，要分类讨论，即可得出结论．
解答：
解：先栽种1，有四种选择，再栽种2，有3种选择，第三步栽种3，有2种选择，第四步栽种4时，要分类讨论，若4栽种的花颜色与2同，则此时5有两种栽种方法，6有一种栽种方法，若4栽种的颜色与2不同，则4有一种栽种方法，若5与2栽种颜色同，则6有两种栽种方法，若5与2不同，则5有一种栽种方法，6也是一种故不同的栽种方法和数是4×3×2×（1×2×1+1×（1×2+1×1））=120种；
故答案为：120．
故答案为：120．
点评：本题考查计数原理的应用，解题的关键是正确理解题意，用加法原理与乘法原理对栽种方法进行计数．本题比较抽象，易因为分类不清或找不到合适的分类方法导致答案错误，故解题时要注意分步与分类是否合理，有没有重复与遗漏的现象．
练习册系列答案
相关题目
甲、乙两人练习射击，命中目标的概率分别为
和
，甲、乙两人各射击一次，目标被命中的概率为（ ）
| 1 |
| 2 |
| 1 |
| 3 |
A、
| ||
B、
| ||
C、
| ||
D、
|
设函数f（x）=（x-1）2+n （x∈[-1，3]，n∈N*）的最小值为an，最大值为bn，记cn=bn2-anbn，则{cn}是（ ）
| A、常数数列 |
| B、公比不为1的等比数列 |
| C、公差不为0的等差数列 |
| D、非等差数列也非等比数列 |