题目内容
设奇函数f（x）在（0，+∞）上为单调递增函数，且f（2）=0，则不等式f（x）≥0的解集为（ ）
| A、[-2，0]∪[2，+∞） |
| B、（-∞，-2]∪（0，2] |
| C、（-∞，-2]∪[2，+∞） |
| D、[-2，0）∪（0，2] |
考点：奇偶性与单调性的综合
专题：不等式的解法及应用
分析：根据函数奇偶性和单调性之间的关系即可得到结论．
解答：
解：f（x）是奇函数，∴f（0）=0，
∵函数f（x）在（0，+∞）上为单调递增函数，且f（2）=0，
∴函数f（x）在（-∞，0）上为单调递增函数，且f（-2）=-f（2）=0，
则当x∈（0，+∞）时，不等式f（x）≥0等价为f（x）≥f（2），此时x≥2，
当x∈（-∞，0）时，不等式f（x）≥0等价为f（x）≥f（-2），此时-2≤x＜0，
综上-2≤x≤0或x≥2，
故选：A
∵函数f（x）在（0，+∞）上为单调递增函数，且f（2）=0，
∴函数f（x）在（-∞，0）上为单调递增函数，且f（-2）=-f（2）=0，
则当x∈（0，+∞）时，不等式f（x）≥0等价为f（x）≥f（2），此时x≥2，
当x∈（-∞，0）时，不等式f（x）≥0等价为f（x）≥f（-2），此时-2≤x＜0，
综上-2≤x≤0或x≥2，
故选：A
点评：本题主要考查不等式的求解，根据函数奇偶性和单调性的关系是解决本题的关键．
练习册系列答案
相关题目
设函数f（x）=（x-1）2+n （x∈[-1，3]，n∈N*）的最小值为an，最大值为bn，记cn=bn2-anbn，则{cn}是（ ）
| A、常数数列 |
| B、公比不为1的等比数列 |
| C、公差不为0的等差数列 |
| D、非等差数列也非等比数列 |
已知等比数列{an}中，a1+a2=3，a2+a3=6，则a8=（ ）
| A、64 | B、128 |
| C、256 | D、512 |
设
为复数z的共轭复数，且
•i=1+2i，则z等于（ ）
. |
| z |
. |
| z |
| A、2-i | B、2+i |
| C、1+2i | D、1-2i |
把函数y=sin（2x+
）的图象向左平移
个单位，再把图象上所有的点的横坐标扩大为原来的2倍，纵坐标缩短为原来的
倍；然后把图象向下平移2个单位．最后得到的函数解析式为：（ ）
| π |
| 3 |
| π |
| 12 |
| 1 |
| 3 |
A、y=
| ||||
| B、y=3cos4x+2 | ||||
C、y=
| ||||
D、y=3sin（4x+
|
若函数f（x）=|x2-k|的图象与函数g（x）=x-3的图象至多有一个公共点，则实数k的取值范围是（ ）
| A、（-∞，3] |
| B、[9，+∞） |
| C、（0，9] |
| D、（-∞，9] |
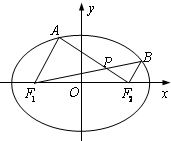如图，在平面直角坐标系xoy中，椭圆