题目内容
已知点P(x,y)的坐标满足
,则(x-1)2+y2的取值范围是( )
|
A、[
| ||
B、[
| ||
| C、[1,9) | ||
D、[
|
考点:简单线性规划
专题:计算题,作图题,不等式的解法及应用
分析:由题意作出其平面区域,(x-1)2+y2可看成阴影内的点到点A(1,0)的距离的平方,求阴影内的点到点A(1,0)的距离的范围可得.
解答:
解:其平面区域如下图:

(x-1)2+y2可看成阴影内的点到点A的距离的平方,
又∵点A到直线x-y=0的距离为:1×
=
,
点A到点B(-2,0)的距离为:3;
设阴影内的点到点A的距离为d,
∴
≤d<3,
∴
≤(x-1)2+y2<9,
故选A.

(x-1)2+y2可看成阴影内的点到点A的距离的平方,
又∵点A到直线x-y=0的距离为:1×
| ||
| 2 |
| ||
| 2 |
点A到点B(-2,0)的距离为:3;
设阴影内的点到点A的距离为d,
∴
| ||
| 2 |
∴
| 1 |
| 2 |
故选A.
点评:本题考查了简单线性规划,作图要细致认真,用到了表达式的几何意义的转化,属于中档题.

练习册系列答案
 智趣寒假作业云南科技出版社系列答案
智趣寒假作业云南科技出版社系列答案
相关题目
设函数f(x)=(x-1)2+n (x∈[-1,3],n∈N*)的最小值为an,最大值为bn,记cn=bn2-anbn,则{cn}是( )
| A、常数数列 |
| B、公比不为1的等比数列 |
| C、公差不为0的等差数列 |
| D、非等差数列也非等比数列 |
若函数f(x)=|x2-k|的图象与函数g(x)=x-3的图象至多有一个公共点,则实数k的取值范围是( )
| A、(-∞,3] |
| B、[9,+∞) |
| C、(0,9] |
| D、(-∞,9] |
已知Sn为等差数列{an}的前n项和,且满足a2+a2013=32,则log2
=( )
| S2014 |
| 2014 |
| A、6 | B、5 | C、4 | D、3 |
点A,B,C,D均在同一球面上,且AB、AC、AD两两垂直,且AB=1,AC=2,AD=3,则该球的表面积为( )
| A、7π | ||||
| B、14π | ||||
C、
| ||||
D、
|
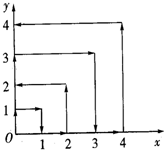 如图,一个质点从原点出发,在与y轴.x轴平行的方向按(0,0)→(0,1)→(1,1)→(1,0)→(2,0)→(2,2)…的规律向前移动,且每秒钟移动一个单位长度,那么到第2011秒时,这个质点所处位置的坐标是( )
如图,一个质点从原点出发,在与y轴.x轴平行的方向按(0,0)→(0,1)→(1,1)→(1,0)→(2,0)→(2,2)…的规律向前移动,且每秒钟移动一个单位长度,那么到第2011秒时,这个质点所处位置的坐标是( )| A、(13,44) |
| B、(14,44) |
| C、(44,13) |
| D、(44,14) |
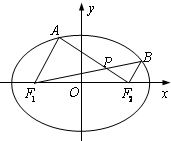 如图,在平面直角坐标系xoy中,椭圆
如图,在平面直角坐标系xoy中,椭圆| x2 |
| 2 |
2
| ||
| 3 |
A、
| ||||
B、
| ||||
C、
| ||||
| D、1 |
执行如图所示的程序框图,如果输入的t∈[-3,3],则输出的S属于( )

| A、[-6,2] |
| B、[-3,16] |
| C、[-4,5] |
| D、[-6,0] |