题目内容
已知△ABC中,AB=
,BC=1,sinC=
cosC,则△ABC的面积为( )
| 3 |
| 3 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
考点:正弦定理
专题:解三角形
分析:根据已知条件求得tanC的值,进而取得C,利用正弦定理求得sinA的值,求得A,利用内角和求得B,最后利用三角形面积公式求得答案.
解答:
解:∵sinC=
cosC,
∴tanC=
,
∴C=
,
∵
=
,
∴sinA=
•sinC=
,
∴A=
或
,
当A=
时,∠C+∠A>π,应舍去.
∴A=
,
∴B=π-
-
=
,即三角形为直角三角形,
∴S△ABC=
AB•BC=
×
×1=
.
故选C
| 3 |
∴tanC=
| 3 |
∴C=
| π |
| 3 |
∵
| BC |
| sinA |
| AB |
| sinC |
∴sinA=
| BC |
| AB |
| 1 |
| 2 |
∴A=
| π |
| 6 |
| 5π |
| 6 |
当A=
| 5π |
| 6 |
∴A=
| π |
| 6 |
∴B=π-
| π |
| 6 |
| π |
| 3 |
| π |
| 2 |
∴S△ABC=
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| ||
| 2 |
故选C
点评:本题主要考查了正弦定理的应用.在求角的时候,一定注意角的范围.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
已知sin2α=
,则cos2(α-
)=( )
| 1 |
| 3 |
| π |
| 4 |
A、-
| ||
B、-
| ||
C、
| ||
D、
|
执行如图所示的程序框图,如输入的p=20,则输出的n的值是( )


| A、3 | B、4 | C、5 | D、6 |
下列求导运算正确的是( )
①(x+
)′=1+
②(log2x)′=
③(3x)′=3xlog3e
④(x2cosx)′=-2xsinx
⑤(
)′=
⑥(exln(2x-5))′=exln(2x-5)+
.
①(x+
| 1 |
| x |
| 1 |
| x2 |
②(log2x)′=
| 1 |
| xln2 |
③(3x)′=3xlog3e
④(x2cosx)′=-2xsinx
⑤(
| ex+1 |
| ex-1 |
| -2ex |
| (ex-1)2 |
⑥(exln(2x-5))′=exln(2x-5)+
| ex |
| 2x-5 |
| A、①②③ | B、②④⑤ |
| C、②⑤ | D、②⑤⑥ |
(x2-1)(
-2)5的展开式的常数项是( )
| 1 |
| x |
| A、48 | B、-48 |
| C、112 | D、-112 |
在△ABC中,已知a=1,b=
,A=30°,B为锐角,那么角A,B,C的大小关系为( )
| 3 |
| A、A.>B>C |
| B、B>A>C |
| C、C>B>A |
| D、C>A>B |
已知某物体的运动曲线方程为:S=2t2-3t-1,则该物体在t=3时的速度为( )
| A、8 | B、9 | C、10 | D、11 |
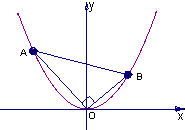 在平面直角坐标系xOy中,抛物线y=x2上异于坐标原点O的两不同动点A、B满足AO⊥BO
在平面直角坐标系xOy中,抛物线y=x2上异于坐标原点O的两不同动点A、B满足AO⊥BO