题目内容
2．
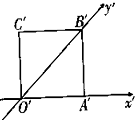如图，正方形O′A′B′C′的边长为2cm，它是水平放置的一个平面图形的直观图，则原平面图形的周长是（ ）cm．| A． | 12 | B． | 16 | C． | $4（1+\sqrt{3}）$ | D． | $4（1+\sqrt{2}）$ |
分析 根据题目给出的直观图的形状，画出对应的原平面图形的形状，求出相应的边长，则问题可求．
解答 
解：由直观图可得原图如图所示，且OA=2，$OB=2O'B'=4\sqrt{2}$，
所以AB=6，所以周长为16，
故选：B．
点评 本题考查了平面图形的直观图，考查了数形结合思想，解答此题的关键是掌握平面图形的直观图的画法，能正确的画出直观图的原图形．
练习册系列答案
相关题目
13．已知正六棱柱的12个顶点都在一个半径为3的球面上，当正六棱柱的体积最大时，其高的值为（ ）
| A． | 3$\sqrt{3}$ | B． | $\sqrt{3}$ | C． | 2$\sqrt{6}$ | D． | 2$\sqrt{3}$ |
10．函数f（x）是定义在（0，+∞）上的单调函数，?x∈（0，+∞），f[f（x）-lnx]=e+1，函数h（x）=xf（x）-ex的最小值为（ ）
| A． | -1 | B． | $-\frac{1}{e}$ | C． | 0 | D． | e |
如图，在直角三角形ABC中，∠B=90°，$AB=\frac{1}{2}AC=1$，点M，N分别在边AB和AC上（M点和B点不重合），将△AMN沿MN翻折，△AMN变为△A'MN，使顶点A'落在边BC上（A'点和B点不重合）．设∠ANM=θ
7．近年来我国电子商务行业发展迅速，相关管理部门推出了针对电商的商品质量和服务评价的评价体系，现从评价系统中选出某商家的200次成功交易，发现对商品质量的好评率为0.6，对服务评价的好评率为0.75，其中对商品质量和服务评价都做出好评的交易80次．
（1）是否可以在犯错误概率不超过0.5%的前提下，认为商品质量与服务好评有关？
（2）若将频率视为概率，某人在该购物平台上进行的5次购物中，设对商品质量和服务评价全好评的次数为随机变量X，求X的分布列（可用组合数公式表示）和数学期望．
参考公式：${k^2}=\frac{{n{{（ad-bc）}^2}}}{（a+b）（c+d）（a+c）（b+d）}$，其中n=a+b+c+d．
（1）是否可以在犯错误概率不超过0.5%的前提下，认为商品质量与服务好评有关？
（2）若将频率视为概率，某人在该购物平台上进行的5次购物中，设对商品质量和服务评价全好评的次数为随机变量X，求X的分布列（可用组合数公式表示）和数学期望．
| P（K2≥k0） | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k0 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
11．函数f（x）=sinx-cosx的图象（ ）
| A． | 关于直线$x=\frac{π}{4}$对称 | B． | 关于直线$x=-\frac{π}{4}$对称 | ||
| C． | 关于直线$x=\frac{π}{2}$对称 | D． | 关于直线$x=-\frac{π}{2}$对称 |
12．若f（x）=xsinx，则函数f（x）的导函数f′（x）等于（ ）
| A． | 1-sinx | B． | x-sinx | C． | sinx+xcosx | D． | cosx-xsinx |