题目内容
13.已知正六棱柱的12个顶点都在一个半径为3的球面上,当正六棱柱的体积最大时,其高的值为( )| A. | 3$\sqrt{3}$ | B. | $\sqrt{3}$ | C. | 2$\sqrt{6}$ | D. | 2$\sqrt{3}$ |
分析 根据正六棱柱和球的对称性,球心O必然是正六棱柱上下底面中心连线的中点,作出过正六棱柱的对角面的轴截面即可得到正六棱柱的底面边长、高和球的半径的关系,在这个关系下求函数取得最值的条件即可求出所要求的量.
解答  解:以正六棱柱的最大对角面作截面,如图.设球心为O,正六棱柱的上下底面中心分别为O1,O2,则O是O1,O2的中点.设正六棱柱的底面边长为a,高为2h,则a2+h2=9.正六棱柱的体积为V=$6×\frac{\sqrt{3}}{4}{a}^{2}×2h$=$3\sqrt{3}(9-{h}^{2})h$,则V′=3$\sqrt{3}$(9-3h2),
解:以正六棱柱的最大对角面作截面,如图.设球心为O,正六棱柱的上下底面中心分别为O1,O2,则O是O1,O2的中点.设正六棱柱的底面边长为a,高为2h,则a2+h2=9.正六棱柱的体积为V=$6×\frac{\sqrt{3}}{4}{a}^{2}×2h$=$3\sqrt{3}(9-{h}^{2})h$,则V′=3$\sqrt{3}$(9-3h2),
得极值点h=$\sqrt{3}$,不难知道这个极值点是极大值点,也是最大值点.故当正六棱柱的体积最大,其高为2$\sqrt{3}$.
故选:D.
点评 本题是在空间几何体、导数的应用交汇处命制,解题的关键是建立正六棱柱体积的函数关系式.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
4.一个几何体的三视图如图所示,则该几何体的表面积是( )
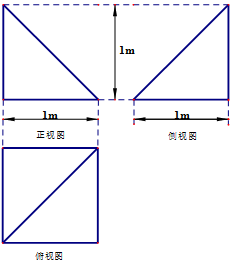

| A. | $(1+\sqrt{2}){m^2}$ | B. | $(1+2\sqrt{2}){m^2}$ | C. | $(2+\sqrt{2}){m^2}$ | D. | $(2+2\sqrt{2}){m^2}$ |
1.已知球O的内接圆柱的体积是2π,底面半径为1,则球O的表面积为( )
| A. | 6π | B. | 8π | C. | 10π | D. | 12π |
8.已知双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$(a>b>0)的一条渐近线方程为y=$\frac{1}{2}$x,则其离心率为( )
| A. | $\frac{\sqrt{5}}{2}$ | B. | $\sqrt{5}$ | C. | $\frac{\sqrt{10}}{2}$ | D. | 2$\sqrt{2}$ |
5.在等差数列{an}中,a1=-6,公差为d,前n项和为Sn,当且仅当n=6时,Sn取得最小值,则d的取值范围为( )
| A. | $(-1,-\frac{7}{8})$ | B. | (0,+∞) | C. | (-∞,0) | D. | $(1,\frac{6}{5})$ |
2.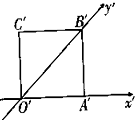 如图,正方形O′A′B′C′的边长为2cm,它是水平放置的一个平面图形的直观图,则原平面图形的周长是( )cm.
如图,正方形O′A′B′C′的边长为2cm,它是水平放置的一个平面图形的直观图,则原平面图形的周长是( )cm.
 如图,正方形O′A′B′C′的边长为2cm,它是水平放置的一个平面图形的直观图,则原平面图形的周长是( )cm.
如图,正方形O′A′B′C′的边长为2cm,它是水平放置的一个平面图形的直观图,则原平面图形的周长是( )cm.| A. | 12 | B. | 16 | C. | $4(1+\sqrt{3})$ | D. | $4(1+\sqrt{2})$ |
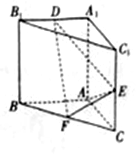 三棱柱ABC-A1B1C1中,AA1⊥平面ABC,AA1=AB=AC=1,E、F分别是CC1、BC的中点,AE⊥A1B1
三棱柱ABC-A1B1C1中,AA1⊥平面ABC,AA1=AB=AC=1,E、F分别是CC1、BC的中点,AE⊥A1B1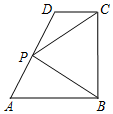 如图,在直角梯形ABCD中,AB∥CD,AB⊥BC,AB=2,CD=1,BC=a(a>0),P为线段AD(含端点)上一个动点,设$\overrightarrow{AP}=x\overrightarrow{AD}$,$\overrightarrow{PB}•\overrightarrow{PC}=y$,则得到函数y=f(x).
如图,在直角梯形ABCD中,AB∥CD,AB⊥BC,AB=2,CD=1,BC=a(a>0),P为线段AD(含端点)上一个动点,设$\overrightarrow{AP}=x\overrightarrow{AD}$,$\overrightarrow{PB}•\overrightarrow{PC}=y$,则得到函数y=f(x).