题目内容
11.函数f(x)=sinx-cosx的图象( )| A. | 关于直线$x=\frac{π}{4}$对称 | B. | 关于直线$x=-\frac{π}{4}$对称 | ||
| C. | 关于直线$x=\frac{π}{2}$对称 | D. | 关于直线$x=-\frac{π}{2}$对称 |
分析 函数解析式提取$\sqrt{2}$,利用两角差的正弦函数公式化简,利用正弦函数图象的性质即可做出判断.
解答 解:函数y=sinx-cosx=$\sqrt{2}$sin(x-$\frac{π}{4}$),
∴x-$\frac{π}{4}$=kπ+$\frac{π}{2}$,k∈Z,得到x=kπ+$\frac{3π}{4}$,k∈Z,
则函数的图象关于直线x=-$\frac{π}{4}$对称.
故选:B.
点评 本题考查了两角差的正弦函数公式,考查正弦函数图象的性质,熟练掌握公式是解本题的关键,是基础题.

练习册系列答案
相关题目
1.已知球O的内接圆柱的体积是2π,底面半径为1,则球O的表面积为( )
| A. | 6π | B. | 8π | C. | 10π | D. | 12π |
2.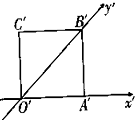 如图,正方形O′A′B′C′的边长为2cm,它是水平放置的一个平面图形的直观图,则原平面图形的周长是( )cm.
如图,正方形O′A′B′C′的边长为2cm,它是水平放置的一个平面图形的直观图,则原平面图形的周长是( )cm.
 如图,正方形O′A′B′C′的边长为2cm,它是水平放置的一个平面图形的直观图,则原平面图形的周长是( )cm.
如图,正方形O′A′B′C′的边长为2cm,它是水平放置的一个平面图形的直观图,则原平面图形的周长是( )cm.| A. | 12 | B. | 16 | C. | $4(1+\sqrt{3})$ | D. | $4(1+\sqrt{2})$ |
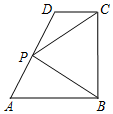 如图,在直角梯形ABCD中,AB∥CD,AB⊥BC,AB=2,CD=1,BC=a(a>0),P为线段AD(含端点)上一个动点,设$\overrightarrow{AP}=x\overrightarrow{AD}$,$\overrightarrow{PB}•\overrightarrow{PC}=y$,则得到函数y=f(x).
如图,在直角梯形ABCD中,AB∥CD,AB⊥BC,AB=2,CD=1,BC=a(a>0),P为线段AD(含端点)上一个动点,设$\overrightarrow{AP}=x\overrightarrow{AD}$,$\overrightarrow{PB}•\overrightarrow{PC}=y$,则得到函数y=f(x).



