题目内容
7.近年来我国电子商务行业发展迅速,相关管理部门推出了针对电商的商品质量和服务评价的评价体系,现从评价系统中选出某商家的200次成功交易,发现对商品质量的好评率为0.6,对服务评价的好评率为0.75,其中对商品质量和服务评价都做出好评的交易80次.(1)是否可以在犯错误概率不超过0.5%的前提下,认为商品质量与服务好评有关?
(2)若将频率视为概率,某人在该购物平台上进行的5次购物中,设对商品质量和服务评价全好评的次数为随机变量X,求X的分布列(可用组合数公式表示)和数学期望.
| P(K2≥k0) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k0 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
分析 (1)由已知列出关于商品和服务评价的2×2列联表,代入公式求得k2的值,对应数表得答案;
(2)每次购物时,对商品和服务全好评的概率为0.4,且X的取值可以是0,1,2,3,4,5,X~B(5,0.4).求出相应的概率,可得对商品和服务全好评的次数X的分布列;利用二项分布的数学期望,求X的数学期望.
解答 解:(1)由题意可得关于商品质量和服务评价的2×2列联表.
| 对服务好评 | 对服务不满意 | 合计 | |
| 商品质量好评 | 80 | 40 | 120 |
| 商品质量不满意 | 70 | 10 | 80 |
| 合计 | 150 | 50 | 200 |
所以${K^2}=\frac{{200×{{(80×10-40×70)}^2}}}{150×50×120×80}=\frac{100}{9}>10.828$,
所以,在犯错误概率不超过0.1%的前提下,认为商品质量与服务好评有关.…(6分)
(2)每次购物时,对商品和服务都好评的概率为$\frac{2}{5}$,且X的取值可以是0,1,2,3,4,5.
其中$P(X=0)={({\frac{3}{5}})^5}$;$P(X=1)=C_5^1({\frac{2}{5}}){({\frac{3}{5}})^4}$;$P(X=2)=C_5^2{({\frac{2}{5}})^2}{({\frac{3}{5}})^3}$;$P(X=3)=C_5^3{({\frac{2}{5}})^3}{({\frac{3}{5}})^2}$;$P(X=4)=C_5^4{({\frac{2}{5}})^4}{({\frac{3}{5}})^1}$;$P(X=5)={({\frac{2}{5}})^5}$.…(10分)
所以X的分布列为
| X | 0 | 1 | 2 | 3 | 4 | 5 |
| P | ${({\frac{3}{5}})^5}$ | $C_5^1({\frac{2}{5}}){({\frac{3}{5}})^4}$ | $C_5^2{({\frac{2}{5}})^2}{({\frac{3}{5}})^3}$ | $C_5^3{({\frac{2}{5}})^3}{({\frac{3}{5}})^2}$ | $C_5^4{({\frac{2}{5}})^4}{({\frac{3}{5}})^1}$ | ${({\frac{2}{5}})^5}$ |
点评 本小题主要考查统计与概率的相关知识,对考生的对数据处理的能力有很高要求,是中档题.

练习册系列答案
 综合自测系列答案
综合自测系列答案
相关题目
2.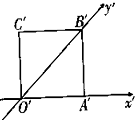 如图,正方形O′A′B′C′的边长为2cm,它是水平放置的一个平面图形的直观图,则原平面图形的周长是( )cm.
如图,正方形O′A′B′C′的边长为2cm,它是水平放置的一个平面图形的直观图,则原平面图形的周长是( )cm.
 如图,正方形O′A′B′C′的边长为2cm,它是水平放置的一个平面图形的直观图,则原平面图形的周长是( )cm.
如图,正方形O′A′B′C′的边长为2cm,它是水平放置的一个平面图形的直观图,则原平面图形的周长是( )cm.| A. | 12 | B. | 16 | C. | $4(1+\sqrt{3})$ | D. | $4(1+\sqrt{2})$ |
12.已知向量$\overrightarrow{AB}=({x,1}),({x>0}),\overrightarrow{AC}=({1,2}),|{\overrightarrow{BC}}|=\sqrt{5}$,则$\overrightarrow{AB},\overrightarrow{AC}$的夹角为( )
| A. | $\frac{2π}{3}$ | B. | $\frac{π}{6}$ | C. | $\frac{π}{4}$ | D. | $\frac{π}{3}$ |
17.已知双曲线$\frac{{x}^{2}}{4}$-$\frac{{y}^{2}}{{b}^{2}}$=1的右焦点与抛物线x=$\frac{{y}^{2}}{12}$的焦点重合,则该双曲线的焦点到其渐近线的距离为( )
| A. | 4$\sqrt{2}$ | B. | $\sqrt{5}$ | C. | 3 | D. | 5 |
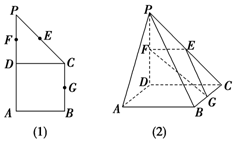 如图(1)所示,在直角梯形ABCP中,BC∥AP,AB⊥BC,CD⊥AP,AD=DC=PD=2,E、F、G分别为线段PC、PD、BC的中点,现将△PDC折起,使平面PDC⊥平面ABCD(图(2)).
如图(1)所示,在直角梯形ABCP中,BC∥AP,AB⊥BC,CD⊥AP,AD=DC=PD=2,E、F、G分别为线段PC、PD、BC的中点,现将△PDC折起,使平面PDC⊥平面ABCD(图(2)).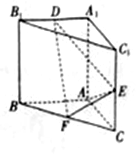 三棱柱ABC-A1B1C1中,AA1⊥平面ABC,AA1=AB=AC=1,E、F分别是CC1、BC的中点,AE⊥A1B1
三棱柱ABC-A1B1C1中,AA1⊥平面ABC,AA1=AB=AC=1,E、F分别是CC1、BC的中点,AE⊥A1B1