题目内容
14．已知抛物线y2=2px（p＞0），过点K（-4，0）作抛物线的两条切线KA，KB，A，B为切点，若AB过抛物线的焦点，△KAB的面积为24，则p的值是（ ）| A． | 12 | B． | -12 | C． | 8 | D． | 4 |
分析 由抛物线的对称性知，AB⊥x轴，且AB是焦点弦，故AB=2p，利用△KAB的面积为24，求出p的值．
解答 解：由抛物线的对称性知，AB⊥x轴，且AB是焦点弦，故AB=2p，
所以${S_{△KAB}}=\frac{1}{2}×2p（{\frac{p}{2}+4}）=24$，解得p=4，
故选：D．
点评 本题考查三角形面积的计算，考查直线与抛物线的位置关系，考查学生分析解决问题的能力，属于中档题．
练习册系列答案
作业辅导系列答案
同步学典一课多练系列答案
经典密卷系列答案
相关题目
4．一个几何体的三视图如图所示，则该几何体的表面积是（ ）
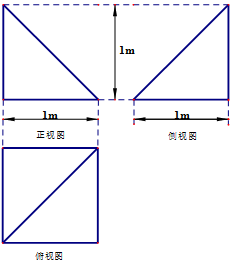
| A． | $（1+\sqrt{2}）{m^2}$ | B． | $（1+2\sqrt{2}）{m^2}$ | C． | $（2+\sqrt{2}）{m^2}$ | D． | $（2+2\sqrt{2}）{m^2}$ |
5．在等差数列{an}中，a1=-6，公差为d，前n项和为Sn，当且仅当n=6时，Sn取得最小值，则d的取值范围为（ ）
| A． | $（-1，-\frac{7}{8}）$ | B． | （0，+∞） | C． | （-∞，0） | D． | $（1，\frac{6}{5}）$ |
2．
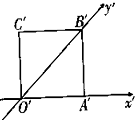如图，正方形O′A′B′C′的边长为2cm，它是水平放置的一个平面图形的直观图，则原平面图形的周长是（ ）cm．
如图，正方形O′A′B′C′的边长为2cm，它是水平放置的一个平面图形的直观图，则原平面图形的周长是（ ）cm．| A． | 12 | B． | 16 | C． | $4（1+\sqrt{3}）$ | D． | $4（1+\sqrt{2}）$ |
9．若复数z满足（1+3i）z=i-3，则z等于（ ）
| A． | i | B． | $\frac{4-3i}{5}$ | C． | -i | D． | $\frac{5}{2}i$ |
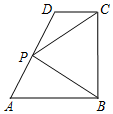如图，在直角梯形ABCD中，AB∥CD，AB⊥BC，AB=2，CD=1，BC=a（a＞0），P为线段AD（含端点）上一个动点，设$\overrightarrow{AP}=x\overrightarrow{AD}$，$\overrightarrow{PB}•\overrightarrow{PC}=y$，则得到函数y=f（x）．
如图所示的几何体中，四边形ABCD是菱形，ADNM是矩形，平面ADNM⊥平面ABCD，∠DAB=$\frac{π}{3}$，AD=4，AM=2，E是AB的中点