题目内容
设数列{an}的前n项和为Sn=n2,{bn}为等比数列,且a1=b1,b2(a2-a1)=b1.
(1)求数列{an}和{bn}的通项公式;
(2)设cn=
,求数列{cn}的前n项和Tn.
(1)求数列{an}和{bn}的通项公式;
(2)设cn=
| 1 |
| anan+1 |
考点:数列的求和
专题:计算题,等差数列与等比数列
分析:(1)由an=
可求得an,易求b1,由b2(a2-a1)=b1可求b2,从而可得公比,进而可得bn;
(2)由(1)可得cn=
=
=
[
-
],由裂项相消法可求得Tn.
|
(2)由(1)可得cn=
| 1 |
| anan+1 |
| 1 |
| (2n-1)(2n+1) |
| 1 |
| 2 |
| 1 |
| 2n-1 |
| 1 |
| 2n+1 |
解答:
解:(1)当n=1时,a1=S1=1;
当n≥2时,an=Sn-Sn-1=n2-(n-1)2=2n-1,
故{an}的通项公式为an=2n-1,即{an}是a1=1,公差d=2的等差数列.
设{bn}的公比为q,则b1=a1=1,又b2(a2-a1)=b1,
∴b2=
∴q=
,
故bn=b1qn-1=1×
,即{bn}的通项公式为bn=
.
(2)∵an=2n-1,
∴cn=
=
=
[
-
],
Tn=
[(1-
)+(
-
)+…+(
-
)]
=
(1-
)
=
.
当n≥2时,an=Sn-Sn-1=n2-(n-1)2=2n-1,
故{an}的通项公式为an=2n-1,即{an}是a1=1,公差d=2的等差数列.
设{bn}的公比为q,则b1=a1=1,又b2(a2-a1)=b1,
∴b2=
| 1 |
| 2 |
| 1 |
| 2 |
故bn=b1qn-1=1×
| 1 |
| 2n-1 |
| 1 |
| 2n-1 |
(2)∵an=2n-1,
∴cn=
| 1 |
| anan+1 |
| 1 |
| (2n-1)(2n+1) |
| 1 |
| 2 |
| 1 |
| 2n-1 |
| 1 |
| 2n+1 |
Tn=
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 5 |
| 1 |
| 2n-1 |
| 1 |
| 2n+1 |
=
| 1 |
| 2 |
| 1 |
| 2n+1 |
=
| n |
| 2n+1 |
点评:本题考查等差数列、等比数列的通项公式及数列求和问题,裂项相消法对数列求和是高考考查的重点内容,要熟练掌握.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
已知f(x)=
,则
的值是( )
| 1 |
| x |
| lim |
| △x→0 |
| -f(2+△x)+f(2) |
| △x |
A、
| ||
| B、2 | ||
C、-
| ||
| D、-2 |
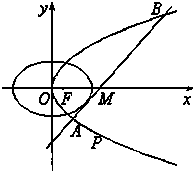 已知椭圆C1和抛物线C2有公共焦点F(1,0),C1的中心和C2的顶点都在坐标原点,过点M(4,0)的直线l与抛物线C2分别相交于A,B两点.
已知椭圆C1和抛物线C2有公共焦点F(1,0),C1的中心和C2的顶点都在坐标原点,过点M(4,0)的直线l与抛物线C2分别相交于A,B两点. 如图,⊙O为四边形ABCD的外接圆,且AB=AD,E是CB延长线上一点,直线EA与圆O相切.求证:
如图,⊙O为四边形ABCD的外接圆,且AB=AD,E是CB延长线上一点,直线EA与圆O相切.求证: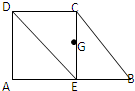 如图所示,已知直角梯形ABCD,AD⊥AB,AB=2AD=2CD,过点C作CE⊥AB于E,G为CE的中点,建立适当的坐标系,用向量的坐标表示法证明:
如图所示,已知直角梯形ABCD,AD⊥AB,AB=2AD=2CD,过点C作CE⊥AB于E,G为CE的中点,建立适当的坐标系,用向量的坐标表示法证明: