题目内容
已知函数f（x）=ax2-2bx+a（a，b∈R）
（1）若a从集合{0，1，2，3}中任取一个元素，b从集合{0，1，2，3}中任取一个元素，求方程f（x）=0恰有两个不相等实根的概率；
（2）若a从区间（0，3）中任取一个数，b从区间（0，2）中任取一个数，求方程f（x）=0没有实根的概率．
（1）若a从集合{0，1，2，3}中任取一个元素，b从集合{0，1，2，3}中任取一个元素，求方程f（x）=0恰有两个不相等实根的概率；
（2）若a从区间（0，3）中任取一个数，b从区间（0，2）中任取一个数，求方程f（x）=0没有实根的概率．
考点：几何概型,古典概型及其概率计算公式
专题：概率与统计
分析：（1）求出方程f（x）=0有两个不相等实根的等价条件，利用古典概型的概率公式，即可得到结论．
（2）作出不等式组对应的平面区域，利用几何概型的概率公式求出相应的面积即可得到结论．
（2）作出不等式组对应的平面区域，利用几何概型的概率公式求出相应的面积即可得到结论．
解答：
解：（1）若方程f（x）=0有两个不相等实根，则△=4b2-4a2＞0，即b2＞a2，∴b＞a，
当a=0时，b=1，2，3，
当a=1时，b=2，3，
当a=2时，b=3，共有6种结果，即满足条件的有6种结果，
则根据古典概型的概率公式可得方程f（x）=0恰有两个不相等实根的概率
=
．
（2）若a从区间（0，3）中任取一个数，b从区间（0，2）中任取一个数，
则0＜a＜3且0＜b＜2，对应的区域为矩形，面积S=3×2=6，
方程f（x）=0没有实根，则△=4b2-4a2＜0，即b2＜a2，∴b＜a，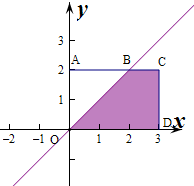
作出不等式组对应的平面区域如图：
则B（2，2），C（3，2），D（3，0），
则题型BCDO的面积S=
×2=4
则由几何概型的概率公式可得方程f（x）=0没有实根
．
当a=0时，b=1，2，3，
当a=1时，b=2，3，
当a=2时，b=3，共有6种结果，即满足条件的有6种结果，
则根据古典概型的概率公式可得方程f（x）=0恰有两个不相等实根的概率
| 6 |
| 4×4 |
| 3 |
| 8 |
（2）若a从区间（0，3）中任取一个数，b从区间（0，2）中任取一个数，
则0＜a＜3且0＜b＜2，对应的区域为矩形，面积S=3×2=6，
方程f（x）=0没有实根，则△=4b2-4a2＜0，即b2＜a2，∴b＜a，
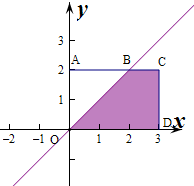
作出不等式组对应的平面区域如图：
则B（2，2），C（3，2），D（3，0），
则题型BCDO的面积S=
| 1+3 |
| 2 |
则由几何概型的概率公式可得方程f（x）=0没有实根
| 4 |
| 6 |
点评：本题主要考查概率的计算，根据古典关系和几何概型的概率公式是解决本题的关键．
练习册系列答案
相关题目
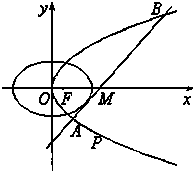已知椭圆C1和抛物线C2有公共焦点F（1，0），C1的中心和C2的顶点都在坐标原点，过点M（4，0）的直线l与抛物线C2分别相交于A，B两点．
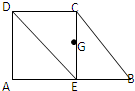如图所示，已知直角梯形ABCD，AD⊥AB，AB=2AD=2CD，过点C作CE⊥AB于E，G为CE的中点，建立适当的坐标系，用向量的坐标表示法证明：
