题目内容
已知二次函数y=ax2+bx+c的图象与两坐标轴的交点分别为（-1，0）和（0，-1），且顶点在y轴的右侧，则实数b的取值范围为 ．
考点：二次函数的性质
专题：函数的性质及应用
分析：先把两点代入函数的表达式得a-b=1，又因顶点在y轴的右侧，从而求出b的范围．
解答：
解：把（-1，0）和（0，-1）代入解析式得：
，
∴a-b=1①，
又顶点在y轴的右侧，
∴-
＞0②，
由①②得：
，
解得：-1＜b＜0，
故答案为：-1＜b＜0．
|
∴a-b=1①，
又顶点在y轴的右侧，
∴-
| b |
| 2a |
由①②得：
|
解得：-1＜b＜0，
故答案为：-1＜b＜0．
点评：本题属于二次函数问题，是一道基础题，解不等式时注意符号．
练习册系列答案
相关题目
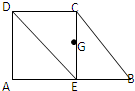如图所示，已知直角梯形ABCD，AD⊥AB，AB=2AD=2CD，过点C作CE⊥AB于E，G为CE的中点，建立适当的坐标系，用向量的坐标表示法证明：
