题目内容
在直角坐标平面内,动点M(x,y)在y轴的左侧,且点M到定点F(-1,0)的距离与到y轴的距离之差为1.
(1)求动点M的轨迹C的方程;
(2)若过点P(-3,-2)的直线l与曲线C交于A、B两点,且点P恰好是AB的中点,求线段AB的长度.
(1)求动点M的轨迹C的方程;
(2)若过点P(-3,-2)的直线l与曲线C交于A、B两点,且点P恰好是AB的中点,求线段AB的长度.
考点:轨迹方程
专题:综合题,圆锥曲线的定义、性质与方程
分析:(1)根据动点M(x,y)在y轴的左侧,且点M到定点F(-1,0)的距离与到y轴的距离之差为1,建立方程,化简可求动点M的轨迹C的方程;
(2)利用点差法求出直线AB的斜率,可得AB的方程美誉抛物线方程联立,结合抛物线的定义,可求线段AB的长度.
(2)利用点差法求出直线AB的斜率,可得AB的方程美誉抛物线方程联立,结合抛物线的定义,可求线段AB的长度.
解答:
解:(1)依题意有:
-(-x)=1…(2分)
即
=1-x,平方化简得:y2=-4x
∴M点的轨迹方程为y2=-4x(x<0)…(4分)
(2)设A(x1,y1),B(x2,y2),
则y12=-4x1,y22=-4x2⇒(y1+y2)(y1-y2)=-4(x1-x2),
∴kAB=
=
=1,
∴lAB:y+2=(x+3)即y=x+1…(8分)
⇒x2+2x+1=-4x⇒x2+6x+1=0,
∴x1+x2=-6,∴|AB|=(1-x1)+(1-x2)=8
即线段AB的长度为8 …(12分)
| (x+1)2+y2 |
即
| (x+1)2+y2 |
∴M点的轨迹方程为y2=-4x(x<0)…(4分)
(2)设A(x1,y1),B(x2,y2),
则y12=-4x1,y22=-4x2⇒(y1+y2)(y1-y2)=-4(x1-x2),
∴kAB=
| y1-y2 |
| x1-x2 |
| -4 |
| -4 |
∴lAB:y+2=(x+3)即y=x+1…(8分)
|
∴x1+x2=-6,∴|AB|=(1-x1)+(1-x2)=8
即线段AB的长度为8 …(12分)
点评:本题考查轨迹方程,考查直线与抛物线的位置关系,考查点差法的运用,属于中档题.

练习册系列答案
相关题目
已知α是第四象限的角,且sinα•cosα=-
,则sinα-cosα=( )
| 12 |
| 25 |
A、-
| ||
B、
| ||
C、
| ||
D、-
|
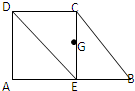 如图所示,已知直角梯形ABCD,AD⊥AB,AB=2AD=2CD,过点C作CE⊥AB于E,G为CE的中点,建立适当的坐标系,用向量的坐标表示法证明:
如图所示,已知直角梯形ABCD,AD⊥AB,AB=2AD=2CD,过点C作CE⊥AB于E,G为CE的中点,建立适当的坐标系,用向量的坐标表示法证明: