题目内容
在锐角△ABC中，sinA=
，cosB=
，求cosC的值．
| 5 |
| 13 |
| 3 |
| 5 |
考点：两角和与差的正弦函数,同角三角函数基本关系的运用
专题：三角函数的求值
分析：利用同角三角函数关系和已知条件分别求得cosA，sinB的值，进而利用cosC=cos（π-A-B）=-cos（A+B）通过两角和公式求得答案．
解答：
解：∵在△ABC中，A，B，C均为锐角，sinA=
，cosB=
，
∴cosA=
=
，sinB=
=
，
∴cosC=cos（π-A-B）
=-cos（A+B）
=-（cosAcosB-sinAsinB）
=-（
×
-
×
）
=-
．
| 5 |
| 13 |
| 3 |
| 5 |
∴cosA=
| 1-sin2A |
| 12 |
| 13 |
| 1-cos2B |
| 4 |
| 5 |
∴cosC=cos（π-A-B）
=-cos（A+B）
=-（cosAcosB-sinAsinB）
=-（
| 12 |
| 13 |
| 3 |
| 5 |
| 5 |
| 13 |
| 4 |
| 5 |
=-
| 16 |
| 65 |
点评：本题主要考查了两角和与差的正弦函数．考查了学生对基本公式的运用．
练习册系列答案
相关题目
如图，⊙O为四边形ABCD的外接圆，且AB=AD，E是CB延长线上一点，直线EA与圆O相切．求证：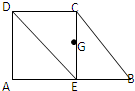
如图所示，已知直角梯形ABCD，AD⊥AB，AB=2AD=2CD，过点C作CE⊥AB于E，G为CE的中点，建立适当的坐标系，用向量的坐标表示法证明：