Question

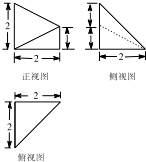某几何体的三视图如图所示，该几何体的表面积是

 

．

Answer 1

考点：由三视图求面积、体积

专题：空间位置关系与距离

分析：根据几何体的三视图得出该几何体是底面为直角梯形的四棱锥，求出它的表面积即可．

解答： 解：根据几何体的三视图得，
该几何体是底面为直角梯形的四棱锥，如图所示；
∴该四棱锥的表面积是
S=

1

2

•2²+

1

2

•（1+2）•2+

1

2

•1•2

2

+

1

2

•2²+

1

2

•1•3=10+

2

．
故答案为：10+

2

．

点评：本题考查了空间几何体的三视图的应用问题，解题时应根据三视图得出该几何体是什么图形，是基础题．