题目内容
已知|
|=1,
•
=
,(
-
)2=
,则|
|= .
| a |
| a |
| b |
| 1 |
| 2 |
| a |
| b |
| 1 |
| 2 |
| b |
考点:平面向量数量积的运算
专题:计算题,平面向量及应用
分析:运用平面向量的数量积的性质:向量的平方即为模的平方,计算即可得到结论.
解答:
解:由于|
|=1,
•
=
,
则(
-
)2=
=
2+
2-2
•
=1+
2-2×
=
2,
即有|
|=
.
故答案为:
.
| a |
| a |
| b |
| 1 |
| 2 |
则(
| a |
| b |
| 1 |
| 2 |
| a |
| b |
| a |
| b |
| b |
| 1 |
| 2 |
| b |
即有|
| b |
| ||
| 2 |
故答案为:
| ||
| 2 |
点评:本题考查平面向量的数量积的性质:向量的平方即为模的平方,考查运算能力,属于基础题.

练习册系列答案
 全优冲刺100分系列答案
全优冲刺100分系列答案 英才点津系列答案
英才点津系列答案
相关题目
函数y=|x|的图象与直线y=a的交点个数( )
| A、至少有一个 |
| B、至多有两个 |
| C、必有两个 |
| D、有一个或两个 |
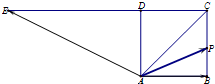 如图,四边形ABCD是边长为1的正方形,延长CD至E,使得DE=2CD.动点P从点A出发,沿正方形的边按逆时针方向运动一周回到A点,
如图,四边形ABCD是边长为1的正方形,延长CD至E,使得DE=2CD.动点P从点A出发,沿正方形的边按逆时针方向运动一周回到A点,