题目内容
直线y=a与曲线y=x2-|x|有四个交点,则a的取值范围是 .
考点:二次函数的图象
专题:函数的性质及应用
分析:作出图象,运用图象判断求解即可.
解答:
解:∵曲线f(x)=x2-|x|,

f(-
)=f(
)=-
,
∴根据图象可得出:直线y=a与曲线y=x2-|x|有四个交点,则-
<a<0

f(-
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 4 |
∴根据图象可得出:直线y=a与曲线y=x2-|x|有四个交点,则-
| 1 |
| 4 |
点评:本题考察了函数的图象,运用图象解决问题,属于中档题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
设曲线y=
在点(-2,f(2))处的切线与直线ax+y+1=0垂直,则实数a=( )
| x-1 |
| x+1 |
A、-
| ||
B、
| ||
| C、-2 | ||
| D、2 |
若函数f(x)=|4x-x2|+2a-8至少有3个零点,则实数a的取值范围是( )
| A、(-∞,3) |
| B、(-∞,3] |
| C、[2,3) |
| D、[2,3] |
在△ABC中,已知6
•
=2
•
=3
•
,则∠A=( )
| AC |
| AB |
| AB |
| BC |
| BC |
| CA |
| A、30° | B、45° |
| C、120° | D、135° |
已知ω>0,函数f(x)=sin(ωx+
)在(
,π)上单调递减,则ω的取值范围是( )
| π |
| 6 |
| π |
| 2 |
A、[
| ||||
B、[
| ||||
C、(0,
| ||||
D、(0,
|
已知:△ABC中,若a2=b2-c2-
ac,则角B=( )
| 3 |
| A、150° | B、120° |
| C、60° | D、30° |
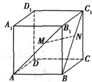 如图,在正方体ABCD-A1B1C1D1中,M、N分别是对角线AB1、BC1上的点,且
如图,在正方体ABCD-A1B1C1D1中,M、N分别是对角线AB1、BC1上的点,且