题目内容
已知集合M={(x1,y1)|y=f(x)},若?(x1,y1)∈M,?(x2,y2)∈M,使得x1x2+y1y2=0成立,则称集合M是“Γ”集.给出下列四个集合:
①M={(x,y)|y=x+
};
②M={(x,y)|y=cosx};
③M={(x,y)|y=ln(x+2)}
④M={(x,y)|y=3x}.
其中是“Γ”集的编号是 .(写出所有是“Γ”集的编号)
①M={(x,y)|y=x+
| 1 |
| x |
②M={(x,y)|y=cosx};
③M={(x,y)|y=ln(x+2)}
④M={(x,y)|y=3x}.
其中是“Γ”集的编号是
考点:函数的图象
专题:新定义,数形结合,函数的性质及应用
分析:本题定义了一个新集合,考查的知识点是借助函数图象性质考查集合的概念,属于元素与集合关系的判断.要证明结论正确,对A(x1,y1)∈M,只要存在B(x1,x2)∈M,使得x1x2+y1y2=0成立,只要
⊥
即可.要说明结论正确,需要证明,否则,举个反例即可.
对于①根据函数图象,图象夹在两条渐近线x=0和y=x之间,即可判断结论不准确.
对于②,画出图象,说明满足“Γ”集合的定义,即可判断正确;
对于③画出函数图象,说明满足“Γ”集合的定义,即可判断正误;
对于④取点A(0,1),不存在点B使得
⊥
,结论不正确.
| OA |
| OB |
对于①根据函数图象,图象夹在两条渐近线x=0和y=x之间,即可判断结论不准确.
对于②,画出图象,说明满足“Γ”集合的定义,即可判断正确;
对于③画出函数图象,说明满足“Γ”集合的定义,即可判断正误;
对于④取点A(0,1),不存在点B使得
| OA |
| OB |
解答:
解:对于①y=x+
的图象是以y轴和直线y=x为渐近线的曲线,渐近线的夹角为45°,如图(1)

在同一支上,任意(x1,y1)∈M,不存在(x2,y2)∈M,满足“Γ”集合的定义;
对任意(x1,y1)∈M,在另一支上也不存在(x2,y2)∈M,使得x1x2+y1y2=0成立,
即
⊥
的两点不存在,所以不满足Γ集合的定义,不是“Γ”集合.
对于②M={(x,y)|y=cosx},如图(2),
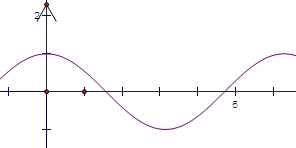
对于任意(x1,y1)∈M,存在(x2,y2)∈M,
使得x1x2+y1y2=0成立,即
⊥
的两点总存在.例如M(0,1)、N( x,0),∠MON=90°,满足Γ集合的定义,旋转90°,都能在图象上找到满足题意的点,所以M是Γ集合;
对于③M={(x,y)|y=ln(x+2)},如图象(3),
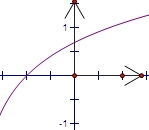
可以看出,M是Γ集合,所以③正确
对于④M═{(x,y)|y=3x},如图(4),
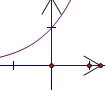
可以证明不满足Γ集合的定义,如点A(0,1),则B(x,0)应在x轴上,可以证明正确.
故答案:②③
| 1 |
| x |

在同一支上,任意(x1,y1)∈M,不存在(x2,y2)∈M,满足“Γ”集合的定义;
对任意(x1,y1)∈M,在另一支上也不存在(x2,y2)∈M,使得x1x2+y1y2=0成立,
即
| OA |
| OB |
对于②M={(x,y)|y=cosx},如图(2),

对于任意(x1,y1)∈M,存在(x2,y2)∈M,
使得x1x2+y1y2=0成立,即
| OA |
| OB |
对于③M={(x,y)|y=ln(x+2)},如图象(3),

可以看出,M是Γ集合,所以③正确
对于④M═{(x,y)|y=3x},如图(4),

可以证明不满足Γ集合的定义,如点A(0,1),则B(x,0)应在x轴上,可以证明正确.
故答案:②③
点评:本题考查Γ集合的定义,画出函数的图象,注意到对于任意(x1,y1)∈M,存在(x2,y2)∈M,使得x1x2+y1y2=0成立,是本题解答的关键,函数的基本性质的考查.

练习册系列答案
相关题目
已知A(2,1),B(1,-2),C(
,-
),动点P(a,b)满足0≤
•
≤2且0≤
•
≤2,则点P到点C的距离大于
的概率为( )
| 3 |
| 5 |
| 1 |
| 5 |
| OP |
| OA |
| OP |
| OB |
| 1 |
| 4 |
A、1-
| ||
B、
| ||
C、1-
| ||
D、
|
 函数f(x)=Asin(ωx+φ)(A,ω,φ为常数,A>0,ω>0,0<φ<π)的图象如图所示,则f(
函数f(x)=Asin(ωx+φ)(A,ω,φ为常数,A>0,ω>0,0<φ<π)的图象如图所示,则f(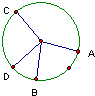 如图,转盘被分成了4部分,其中∠AOB=∠COD=90°,则随意转动转盘,指针指向∠AOB和∠COD所在区域的概率是
如图,转盘被分成了4部分,其中∠AOB=∠COD=90°,则随意转动转盘,指针指向∠AOB和∠COD所在区域的概率是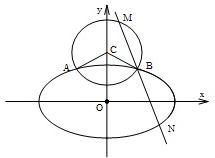 已知离心率为
已知离心率为