Question

已知A（2，1），B（1，-2），C（

3

5

，-

1

5

），动点P（a，b）满足0≤

OP

•

OA

≤2且0≤

OP

•

OB

≤2，则点P到点C的距离大于

1

4

的概率为（　　）

• A、1-

  5

  64

  π
• B、

  5

  64

  π
• C、1-

  π

  16

• D、

  π

  16

Answer 1

考点：几何概型

专题：概率与统计

分析：根据向量的数量积的坐标公式将不等式进行化简，作出不等式组对应的平面区域，利用几何概型的概率公式即可得到结论．

解答： 解：∵A（2，1），B（1，-2），C（

3

5

，-

1

5

），P（a，b）
∴

OP

•

OA

=2a+b，且

OP

•

OB

=a-2b，
∵0≤

OP

•

OA

≤2且0≤

OP

•

OB

≤2，
∴0≤2a+b≤2且0≤a-2b≤2，
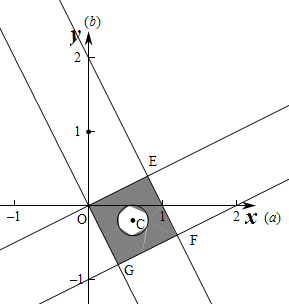
作出不等式组对应的平面区域如图：
∵点P到点C的距离大于

1

4

，
∴|CP|＞

1

4

，则对应的部分为阴影部分，
由

a-2b=0 2a+b=2

解得

a= 4 5 b= 2 5

，
即E（

4

5

，

2

5

），|OE|=

( 4 5 )2+( 2 5 )2

=

20 25

=

4 5

，
∴正方形OEFG的面积为

4 5

×

4 5

=

4

5

，
则阴影部分的面积为

4

5

-π×(

1

4

)2=

4

5

-

π

16

，
∴根据几何概型的概率公式可知所求的概率为

4 5 - π 16

4 5

=1-

5π

64

，
故选：A．

点评：本题主要考查几何概型的概率公式的计算，利用数量积将不等式进行转化，求出相应区域的面积是解决本题的关键．