题目内容
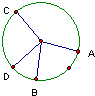如图，转盘被分成了4部分，其中∠AOB=∠COD=90°，则随意转动转盘，指针指向∠AOB和∠COD所在区域的概率是考点：几何概型
专题：概率与统计
分析：设圆的半径为r，根据题意，易得S扇形AOB与S扇形COD的面积，进而可得两部分的面积和，由几何概率的求法，可得答案．
解答：
解：设圆的半径为r，
根据题意，有一转盘被分成四部分，其中∠AOB=∠COD=90°，
有∠AOB+∠COD=180°，
S扇形AOB=S扇形COD=
π r2，
则S扇形AOB+S扇形COD=
πr2，
故指针指向∠AOB和∠COD所在区域的概率是
=
；
故答案为：
．
根据题意，有一转盘被分成四部分，其中∠AOB=∠COD=90°，
有∠AOB+∠COD=180°，
S扇形AOB=S扇形COD=
| 1 |
| 4 |
则S扇形AOB+S扇形COD=
| 1 |
| 2 |
故指针指向∠AOB和∠COD所在区域的概率是
| ||
| πr2 |
| 1 |
| 2 |
故答案为：
| 1 |
| 2 |
点评：此题考查几何概率的求法，事件（A）所表示的区域的面积与总面积的值，就是事件（A）发生的概率．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
如图所示，边长为2的正方形中有一封闭曲线围成的阴影区域，在正方形中随机撒一粒豆子，若它落在阴影区域内的概率为在区间[0，2]之间随机抽取一个数x，则x满足2x-1≥0的概率为（ ）
A、
| ||
B、
| ||
C、
| ||
D、
|