题目内容
在平面直角坐标系xOy中,双曲线C的中心在原点,焦点在y轴上,一条渐近线方程为x-
y=0,则双曲线C的离心率为 .
| 3 |
考点:双曲线的简单性质
专题:圆锥曲线的定义、性质与方程
分析:由已知条件推导出双曲线方程为y2-
=λ,λ>0,由此能求出双曲线的离心率.
| x2 |
| 3 |
解答:
解:∵双曲线C的中心在原点,焦点在y轴上,
一条渐近线方程为x-
y=0,
∴双曲线方程为y2-
=λ,λ>0,
∴双曲线的标准方程为
-
=1,
∴a=
,c=
=2
,
∴e=
=2.
故答案为:2.
一条渐近线方程为x-
| 3 |
∴双曲线方程为y2-
| x2 |
| 3 |
∴双曲线的标准方程为
| y2 |
| λ |
| x2 |
| 3λ |
∴a=
| λ |
| 4λ |
| λ |
∴e=
| c |
| a |
故答案为:2.
点评:本题考查双曲线的离心率的求法,是中档题,解题时要熟练掌握双曲线的简单性质.

练习册系列答案
 愉快的寒假南京出版社系列答案
愉快的寒假南京出版社系列答案
相关题目
“m<1”是“方程x2+2x+m=0有实数解的( )条件.
| A、充分必要 |
| B、充分不必要 |
| C、必要不充分 |
| D、既不充分也不必要 |
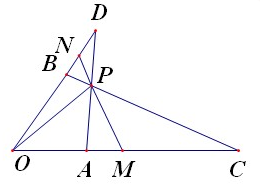 如图,
如图,