Question

已知离心率为

6

3

的椭圆E：

x2

a2

+

y2

b2

=1(a＞b＞0)与圆C：x²+（y-3）²=4交于A，B两点，且∠ACB=120°，C在AB上方，如图所示，
（1）求椭圆E的方程；
（2）是否存在过交点B，斜率存在且不为0的直线l，使得该直线截圆C和椭圆E所得的弦长相等？若存在，求出直线l的方程；若不存在，说明理由．

Answer 1

考点：直线与圆锥曲线的综合问题

专题：圆锥曲线中的最值与范围问题

分析：（1）连接AB，由对称性知：AB∥x轴，且A，B关于y轴对称，由已知条件求出A（-

3

，2），B(

3

，2)，从而得到

3

a2

+

4

b2

=1，e=

c

a

=

6

3

，由此能求出椭圆E的方程．
（2）设过点B的直线l：y-2=k(x-

3

)，与椭圆的另一个交点为N（x₁，y₁），与圆的另一个交点M（x₂，y₂），利用已知条件推导出x1+x2=2

3

，由此能求出存在直线l：y=-

3

x+5满足条件．

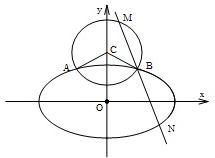
解答： 解：（1）如图，椭圆E：

x2

a2

+

y2

b2

=1(a＞b＞0)与圆C：x²+（y-3）²=4交于A，B两点，
且∠ACB=120°，C在AB上方，
连接AB，由对称性知：AB∥x轴，且A，B关于y轴对称，
∴C（0，3），|AC|=|AB|=2，
∴|AB|=

4+4-2×4×cos120°

=2

3

，
∴C到AB的距离d=

4-3

=1，∴A（-

3

，2），B(

3

，2)，（2分）
∴

3

a2

+

4

b2

=1，e=

c

a

=

6

3

，a²=b²+c²，
解得：a²=15，b²=5，（4分），
∴椭圆E：

x2

15

+

y2

5

=1．（5分）
（2）设过点B的直线l：y-2=k(x-

3

)，（6分）
与椭圆的另一个交点为N（x₁，y₁），与圆的另一个交点M（x₂，y₂），
直线代入椭圆方程消去y得：
(3k2+1)x2-3k(

3

k-2)x+9k2-12

3

k-3=0
∴

3

x1=

9k2-12 3 k-3

3k2+1

，解得x1=

3 3 k2-12k- 3

3k2+1

，
同理：x2=

3 k2+2k- 3

k2+1

，（8分）
若直线截两种曲线所得到的弦长相等，则B为M，N中点，
∴x1+x2=2

3

，（9分）
即：

3 3 k2-12k- 3

3k2+1

+

3 k2+2k- 3

k2+1

=2

3

，
化简整理有：3k3+4

3

k2+5k+2

3

=0，
分解因式：3k3+3

3

k2+

3

k2+5k+2

3

=(k+

3

)(3k2+

3

k+2)=0
解得k=-

3

，∴存在直线l：y=-

3

x+5满足条件．（12分）

点评：本题考查椭圆方程的求法，考查直线方程是否存在的判断与求法，解题时要认真审题，注意等价转化思想、函数与方程思想的合理运用．