题目内容
5．求满足下列条件的直线方程．（1）直线l1经过点A（4，-2），B（-1，8）；
（2）直线l2过点C（-2，1），且与y轴平行．
分析 （1）由两点式方程知，直线l1的方程；
（2）根据直线l2过点C（-2，1），且与y轴平行，可得结论．
解答 解：（1）由两点式方程知，直线l1的方程为$\frac{y-（-2）}{8-（-2）}=\frac{x-4}{-1-4}$，
化简有2x+y-6=0…（4分）
（2）由题意知直线l2的方程为x=-2…（8分）
点评 本题考查直线方程，考查学生的计算能力，比较基础．
练习册系列答案
相关题目
15．直线x=tan45°的倾斜角为（ ）
| A． | 0° | B． | 45° | C． | 90° | D． | 不存在 |
10．下列命题正确的是（ ）
| A． | 到x轴距离为5的点的轨迹是y=5 | |
| B． | 方程$\frac{x}{y}=1$表示的曲线是直角坐标平面上第一象限的角平分线 | |
| C． | 方程（x-y）2+（xy-1）2=0表示的曲线是一条直线和一条双曲线 | |
| D． | 2x2-3y2-2x+m=0通过原点的充要条件是m=0 |
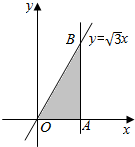如图，在平面直角坐标系xOy中，直线y=$\sqrt{3}$x，y=0，x=t（t＞0）围成的△OAB的面积为S（t），则S（t）在t=2时的瞬时变化率是2$\sqrt{3}$．