题目内容
13.设等差数列{an}的前n项和为Sn,且a2=3,S6=36.(Ⅰ)求数列{an}的通项公式;
(Ⅱ)令bn=$\frac{4n}{{{a}_{n}}^{2}{{a}_{n+1}}^{2}}$,求数列{an}的前n项和Tn.
分析 (I)利用等差数列通项公式及其前n项和公式即可得出;
(II)利用“裂项求和”即可得出.
解答 解:(I)设等差数列{an}的公差为d,∵a2=3,S6=36.
∴$\left\{\begin{array}{l}{{a}_{1}+d=3}\\{6{a}_{1}+\frac{6×5}{2}d=36}\end{array}\right.$,解得a1=1,d=2.
∴an=1+2(n-1)=2n-1.
(II)bn=$\frac{4n}{{{a}_{n}}^{2}{{a}_{n+1}}^{2}}$=$\frac{4n}{(2n-1)^{2}(2n+1)^{2}}$=$\frac{1}{2}$($\frac{1}{(2n-1)^{2}}-\frac{1}{(2n+1)^{2}}$),
∴数列{an}的前n项和Tn=$\frac{1}{2}[(1-\frac{1}{{3}^{2}})$+$(\frac{1}{{3}^{2}}-\frac{1}{{5}^{2}})$+…+$(\frac{1}{(2n-1)^{2}}-\frac{1}{(2n+1)^{2}})]$
=$\frac{1}{2}$$[1-\frac{1}{(2n+1)^{2}}]$
=$\frac{2{n}^{2}+2n}{(2n+1)^{2}}$.
点评 本题考查了等差数列的通项公式及其前n项和公式、“裂项求和”方法,考查了推理能力与计算能力,属于中档题.

练习册系列答案
 阳光课堂同步练习系列答案
阳光课堂同步练习系列答案
相关题目
4.命题P:“A>30°”是命题Q:“sinA>$\frac{1}{2}$”的( )条件.
| A. | 充要 | B. | 必要不充分 | ||
| C. | 充分不必要 | D. | 既不充分也不必要 |
18.设各项均为正数的数列{an}的前n项之积为Tn,若${T_n}={2^{{n^2}+n}}$,则$\frac{{{a_n}+12}}{2^n}$的最小值为( )
| A. | 7 | B. | 8 | C. | $4\sqrt{3}$ | D. | $2\sqrt{3}$ |
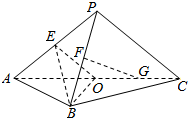 如图,平面PAC⊥平面ABC,△ABC是以AC为斜边的等腰直角三角形,E,F,O分别为PA,PB,AC的中点,AC=16,PA=PC=10.
如图,平面PAC⊥平面ABC,△ABC是以AC为斜边的等腰直角三角形,E,F,O分别为PA,PB,AC的中点,AC=16,PA=PC=10.