如图.在平面直角坐标系xOy中.直线y=$\sqrt{3}$x.y=0.x=t围成的△OAB的面积为S在t=2时的瞬时变化率是2$\sqrt{3}$．题目和参考答案——青夏教育精英家教网—

题目内容

17．

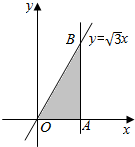如图，在平面直角坐标系xOy中，直线y=$\sqrt{3}$x，y=0，x=t（t＞0）围成的△OAB的面积为S（t），则S（t）在t=2时的瞬时变化率是2$\sqrt{3}$．

分析先用t表示出三角形的面积，再求导，代值计算即可．

解答解：由|AB|=$\sqrt{O{B}^{2}-O{A}^{2}}$=$\sqrt{3}$t，
∴S（t）=$\frac{1}{2}$|OA|•|OB|=$\frac{1}{2}$$\sqrt{3}$t•t=$\frac{\sqrt{3}}{2}$t²，
∴S′（t）=$\sqrt{3}$t，
∴S′（2）=2$\sqrt{3}$，
故答案为：2$\sqrt{3}$．

点评本题考查了三角形的面积公式和导数瞬时变化率的几合意义，属于基础题．

练习册系列答案

河北考王赢在中考系列答案

鸿鹄志文化期末冲刺王寒假作业系列答案

名题教辅寒假作业快乐衔接武汉出版社系列答案

名榜文化假期作业寒假郑州大学出版社系列答案

8．已知函数y=-x³+3x+c的图象与x轴恰有两个不同公共点，则实数c的值为±2．

5．求满足下列条件的直线方程．
（1）直线l₁经过点A（4，-2），B（-1，8）；
（2）直线l₂过点C（-2，1），且与y轴平行．

12．下列五个命题中，
①点P（-1，4）到直线3x+4y=2的距离为3．
②过点M（-3，5）且在两坐标轴上的截距互为相反数的直线方程为x-y+8=0．
③在正方体ABCD-A₁B₁C₁D₁中，E，F分别是AB，AD的中点，则异面直线B₁C与EF所成的角的大小60°
④过点（-3，0）和点（-4，$\sqrt{3}$）的直线的倾斜角是120°
⑤直线x+2y+3=0与直线2x+4y+1=0的距离是$\frac{{\sqrt{5}}}{2}$．
其中正确的个数是（　　）

2．给出下列四个命题：
①f（x）=x³-3x²是增函数，无极值．
②f（x）=x³-3x²在（-∞，2）上没有最大值
③若命题p：a=0是复数z=a+bi（a，b∈R）为纯虚数的充分条件，命题q：f′（x₀）=0是“点x₀是可导函数f（x）的极值点”的必要条件，则￢p∧q为真．
④设z₁，z₂是复数，z₁²+z₂²=0?z₁=z₂=0
其中正确命题的个数为（　　）

9．在正方体ABCD-A′B′C′D′中，判断下列命题是否正确，并说明理由：
（1）直线AC在平面ABCD内；
（2）设上下底面中心为O，O′，则平面AA′C′C与平面BB′D′D的交线为OO′．
（3）点A，O，C′可以确定一平面．
（4）平面AB′C′与平面AC′D重合．

6．设函数f（x）=1n（x+1）+a（x²-x），其中a∈R，当a=1时，求函数f（x）的极值．

7．已知f（x）=$\left\{\begin{array}{l}{{2}^{|x-1|}-1，x≤2}\\{\frac{1}{2}f（x-2），x＞2}\end{array}\right.$，g（x）=log_ax（a＞1），若F（x）=f（x）-g（x）恰有三个不同零点，则实数a的取值范围为（4，${e}^{\frac{1}{ln2}}$）∪[16，256]．（参考值：ln2≈0.7 ）

试题分类