题目内容
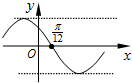 若函数f(x)=sin(ωx+φ)-cos(ωx+φ) (ω>0,0<φ<2π),满足f(x+
若函数f(x)=sin(ωx+φ)-cos(ωx+φ) (ω>0,0<φ<2π),满足f(x+| π |
| 3 |
| π |
| 3 |
(Ⅰ)求f(x)解析式;
(Ⅱ)若α∈(π,2π),且f(
| α |
| 3 |
| π |
| 12 |
| α |
| 3 |
| π |
| 12 |
考点:由y=Asin(ωx+φ)的部分图象确定其解析式
专题:三角函数的图像与性质
分析:(Ⅰ)由周期求出ω,由特殊点的坐标求出φ的值,可得f(x)解析式.
(Ⅱ)根据条件,利用三角恒等变换求出sin(α-
)=
,可得α=
+
,从而求得cosα的值.
(Ⅱ)根据条件,利用三角恒等变换求出sin(α-
| π |
| 4 |
| 1 |
| 2 |
| 5π |
| 6 |
| π |
| 4 |
解答:
解:( I )依题设f(x+
)=f(x-
)知:f(x+
)=f(x),可得f(x)的周期T=
,故ω=3.
故f(x)=sin(3x+φ)-cos(3x+φ)=
sin(3x+φ-
).
又点(
,0)在其图象上,可得
sinφ=0,求得sinφ=0,
又0<φ<2π,可得φ=π,故f(x)=-
sin(3x-
)为所求.
( II )依题设及( I )知:f(
+
)+f(
-
)=-
sinα-
sin(α-
)=-1.
整理得:
sinα-
cosα=1,求出sin(α-
)=
.
又依题设:α∈(π,2π),可得α-
=
,求得α=
+
.
故cosα=cos(
+
)=-
为所求.
| π |
| 3 |
| π |
| 3 |
| 2π |
| 3 |
| 2π |
| 3 |
故f(x)=sin(3x+φ)-cos(3x+φ)=
| 2 |
| π |
| 4 |
又点(
| π |
| 12 |
| 2 |
又0<φ<2π,可得φ=π,故f(x)=-
| 2 |
| π |
| 4 |
( II )依题设及( I )知:f(
| α |
| 3 |
| π |
| 12 |
| α |
| 3 |
| π |
| 12 |
| 2 |
| 2 |
| π |
| 2 |
整理得:
| 2 |
| 2 |
| π |
| 4 |
| 1 |
| 2 |
又依题设:α∈(π,2π),可得α-
| π |
| 4 |
| 5π |
| 6 |
| 5π |
| 6 |
| π |
| 4 |
故cosα=cos(
| 5π |
| 6 |
| π |
| 4 |
| ||||
| 4 |
点评:本题主要考查三角恒等变换,由函数y=Asin(ωx+φ)的部分图象求解析式,由周期求出ω,由特殊点的坐标求出φ的值,属于基础题.

练习册系列答案
 赢在课堂名师课时计划系列答案
赢在课堂名师课时计划系列答案 天天向上课时同步训练系列答案
天天向上课时同步训练系列答案
相关题目
已知y=f(x)+x2是奇函数,且f(1)=1,若g(x)=f(x)+2,则g(-1)=( )
| A、-1 | B、0 | C、1 | D、2 |
在数列{an}中,a1=-
,an=1-
(n>1),则a2014的值为( )
| 1 |
| 4 |
| 1 |
| an-1 |
A、-
| ||
| B、5 | ||
C、
| ||
| D、以上都不对 |
函数y=
+
的定义域为( )
| 1+x |
| x |
| A、{x|x≤1} |
| B、{x|x≥0} |
| C、{x|x≥1或x≤0} |
| D、{x|0≤x≤1} |
 在如图所示的几何体中,四边形ABCD是直角梯形,AD∥BC,AB⊥BC,AD=2,AB=3,BC=BE=7,△DCE是边长为6的正三角形.
在如图所示的几何体中,四边形ABCD是直角梯形,AD∥BC,AB⊥BC,AD=2,AB=3,BC=BE=7,△DCE是边长为6的正三角形.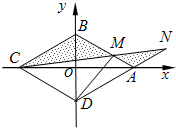 如图,菱形ABCD的边长为2,∠BAD=60°,M为AB边上不与端点重合的动点,且CM与DA分别延长后交于点N,若以菱形的对角线所在直线为坐标轴建立平面直角坐标系,并设BM=2t (0<t<1).
如图,菱形ABCD的边长为2,∠BAD=60°,M为AB边上不与端点重合的动点,且CM与DA分别延长后交于点N,若以菱形的对角线所在直线为坐标轴建立平面直角坐标系,并设BM=2t (0<t<1).