题目内容
 在如图所示的几何体中,四边形ABCD是直角梯形,AD∥BC,AB⊥BC,AD=2,AB=3,BC=BE=7,△DCE是边长为6的正三角形.
在如图所示的几何体中,四边形ABCD是直角梯形,AD∥BC,AB⊥BC,AD=2,AB=3,BC=BE=7,△DCE是边长为6的正三角形.(1)求证:平面DEC⊥平面BDE;
(2)求二面角C-BE-D的余弦值.
考点:平面与平面垂直的判定,二面角的平面角及求法
专题:
分析:(1)根据勾股定理证明BD⊥CD,BD⊥DE,可得BD⊥平面DEC,利用平面与平面垂直的判定定理,即可证明平面DEC⊥平面BDE;
(2)求出S△CBE、S△BED,即可求二面角C-BE-D的余弦值.
(2)求出S△CBE、S△BED,即可求二面角C-BE-D的余弦值.
解答:
(1)证明:因为四边形ABCD为直角梯形,
AD∥BC,AB⊥BC,AD=2,AB=3,所以BD=
,
又因为BC=7,CD=6,所以根据勾股定理可得BD⊥CD,
因为BE=7,DE=6,同理可得BD⊥DE.
因为DE∩CD=D,DE?平面DEC,CD?平面DEC,
所以BD⊥平面DEC.
因为BD?平面BDE,
所以平面DEC⊥平面BDE;
(2)解:在△CBE中,BC=7,CE=6,BE=7,∴S△CBE=
×6×
=6
,
在△BED中,BD=
,DE=6,BE=7,∴S△BED=
×6×
=3
,
∴二面角C-BE-D的余弦值为
=
.
AD∥BC,AB⊥BC,AD=2,AB=3,所以BD=
| 13 |
又因为BC=7,CD=6,所以根据勾股定理可得BD⊥CD,
因为BE=7,DE=6,同理可得BD⊥DE.
因为DE∩CD=D,DE?平面DEC,CD?平面DEC,
所以BD⊥平面DEC.
因为BD?平面BDE,
所以平面DEC⊥平面BDE;
(2)解:在△CBE中,BC=7,CE=6,BE=7,∴S△CBE=
| 1 |
| 2 |
| 49-9 |
| 10 |
在△BED中,BD=
| 13 |
| 1 |
| 2 |
| 13 |
| 13 |
∴二面角C-BE-D的余弦值为
3
| ||
6
|
| ||
| 20 |
点评:本题考查平面与平面垂直,考查二面角C-BE-D的余弦值,考查学生分析解决问题的能力,属于中档题.

练习册系列答案
相关题目
已知m=a+
(a>2),n=2 2-b2(b≠0),则m,m的大小关系是( )
| 1 |
| a-2 |
| A、m>n | B、m<n |
| C、m=n | D、不确定 |
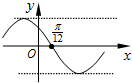 若函数f(x)=sin(ωx+φ)-cos(ωx+φ) (ω>0,0<φ<2π),满足f(x+
若函数f(x)=sin(ωx+φ)-cos(ωx+φ) (ω>0,0<φ<2π),满足f(x+