题目内容
已知△ABC的三边长a，b，c依次成等差数列，a2+b2+c2=21，则b的取值范围是 ．
考点：等差数列的性质
专题：计算题,等差数列与等比数列
分析：设a=b-d，c=b+d，代入已知等式化简可得3b2+2d2=21，由此求得b的最大值为
．再由a+b＞c 可得b＞2d，结合已知的等式得3b2+2(
)2＞21，解得b＞
，再把这两个b的范围取交集求得数b的取值范围．
| 7 |
| b |
| 2 |
| 6 |
解答：
解：设公差为d，则有 a=b-d，c=b+d，代入a2+b2+c2=21化简可得3b2+2d2=21．
故当d=0时，b有最大值为
．
由于三角形任意两边之和大于第三边，故较小的两边之和大于最大边，即a+b＞c，可得b＞2d．
∴3b2+2(
)2＞21，解得b＞
，
故实数b的取值范围是（
，
]．
故答案为 （
，
]．
故当d=0时，b有最大值为
| 7 |
由于三角形任意两边之和大于第三边，故较小的两边之和大于最大边，即a+b＞c，可得b＞2d．
∴3b2+2(
| b |
| 2 |
| 6 |
故实数b的取值范围是（
| 6 |
| 7 |
故答案为 （
| 6 |
| 7 |
点评：本题主要考查等差数列的定义和性质的应用，解不等式，属于中档题．
练习册系列答案
津桥教育计算小状元系列答案
相关题目
定义在R上的函数满足f（x+y）=f（x）+f（y），且在区间（0，+∞）上单调递增，若实数a满足2f（log2a）+f（log
a）≤f（1），则a的取值范围是（ ）
| 1 |
| 2 |
| A、[1，2] | ||
B、（0，
| ||
| C、（0，2] | ||
| D、（-∞，2] |
若集合M={y|y=2x}，N={y|y=logx}，则M∩N=（ ）
| A、{x|x＞1} |
| B、{y|y≥1} |
| C、{x|x＞0} |
| D、{y|y≥0} |
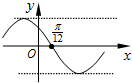若函数f（x）=sin（ωx+φ）-cos（ωx+φ） （ω＞0，0＜φ＜2π），满足f（x+