题目内容
函数y=
+
的定义域为( )
| 1+x |
| x |
| A、{x|x≤1} |
| B、{x|x≥0} |
| C、{x|x≥1或x≤0} |
| D、{x|0≤x≤1} |
考点:函数的定义域及其求法
专题:函数的性质及应用
分析:求该函数的定义域,直接让x+1≥0,x≥0求解x即可.
解答:
解:由
,得:x≥0.
所以原函数的定义域为[0,+∞).
故答案为[0,+∞).
故选B.
|
所以原函数的定义域为[0,+∞).
故答案为[0,+∞).
故选B.
点评:本题考查了函数定义域的求法,解答的关键是让根式内部的代数式大于等于0,属基础题.

练习册系列答案
 黄冈小状元解决问题天天练系列答案
黄冈小状元解决问题天天练系列答案 三点一测快乐周计划系列答案
三点一测快乐周计划系列答案
相关题目
若{an}是等差数列,首项a1>0,a1007+a1008>0,a1007•a1008<0,则使前n项和Sn>0成立的最大自然数n是( )
| A、2012 | B、2013 |
| C、2014 | D、2015 |
已知m=a+
(a>2),n=2 2-b2(b≠0),则m,m的大小关系是( )
| 1 |
| a-2 |
| A、m>n | B、m<n |
| C、m=n | D、不确定 |
已知sinx+siny=
,则u=sinx+cos2x的最小值是( )
| 1 |
| 3 |
A、-
| ||
| B、-1 | ||
| C、1 | ||
D、
|
设函数y=f(2x)的定义域是[-1,0],则y=f(2x-1)的定义域是( )
| A、[-1,0] | ||||
B、[-
| ||||
| C、[-2,0] | ||||
| D、[-3,-1] |
已知双曲线
-
=1的实轴长、虚轴长、焦距依次成等比数列,则其离心率为( )
| x2 |
| a2 |
| y2 |
| b2 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
设集合A={0,1},B={-1,0,m-2},若A⊆B,则实数m=( )
| A、0 | B、1 | C、2 | D、3 |
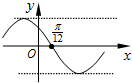 若函数f(x)=sin(ωx+φ)-cos(ωx+φ) (ω>0,0<φ<2π),满足f(x+
若函数f(x)=sin(ωx+φ)-cos(ωx+φ) (ω>0,0<φ<2π),满足f(x+