题目内容
f(x)是定义在R上的奇函数,当x∈(0,1)时,f(x)=
.
(1)求f(x)在(-1,0)上的解析式
(2)证明:f(x)在(0,1)上是减函数.
| 2x |
| 4x+1 |
(1)求f(x)在(-1,0)上的解析式
(2)证明:f(x)在(0,1)上是减函数.
考点:函数单调性的判断与证明,函数解析式的求解及常用方法
专题:函数的性质及应用
分析:(1)设x∈(-1,0),则-x∈(0,1),由已知式子和函数的奇偶性可得;(2)定义法:任取0<x1<x2<1,变形可得f(x2)-f(x1)<0,可判函数的单调性.
解答:
解:(1)设x∈(-1,0),则-x∈(0,1),
∵x∈(0,1)时,f(x)=
,
∴f(-x)=
=
,
又∵f(x)为奇函数知,
∴-f(x)=
,∴f(x)=-
.
∴当x∈(-1,0)时,f(x)=-
;
(2)证明:任取0<x1<x2<1,
则f(x2)-f(x1)=
-
=
,
∵0<x1<x2<1,∴2x1-2x2<0,
又4x1+1>0,4x2+1>0,2x1+x2-1>0
∴f(x2)-f(x1)<0,即f(x2)<f(x1).
∴f(x)在(0,1)上是减函数.
∵x∈(0,1)时,f(x)=
| 2x |
| 4x+1 |
∴f(-x)=
| 2-x |
| 4-x+1 |
| 2x |
| 4x+1 |
又∵f(x)为奇函数知,
∴-f(x)=
| 2x |
| 4x+1 |
| 2x |
| 4x+1 |
∴当x∈(-1,0)时,f(x)=-
| 2x |
| 4x+1 |
(2)证明:任取0<x1<x2<1,
则f(x2)-f(x1)=
| 2x2 |
| 4x2+1 |
| 2x1 |
| 4x1+1 |
=
| (2x1+x2-1)(2x1-2x2) |
| (4x1+1)(4x2+1) |
∵0<x1<x2<1,∴2x1-2x2<0,
又4x1+1>0,4x2+1>0,2x1+x2-1>0
∴f(x2)-f(x1)<0,即f(x2)<f(x1).
∴f(x)在(0,1)上是减函数.
点评:本题考查函数的单调性的判断与证明,涉及函数解析式的求解,属基础题.

练习册系列答案
 学练快车道口算心算速算天天练系列答案
学练快车道口算心算速算天天练系列答案
相关题目
定义在R上的函数满足f(x+y)=f(x)+f(y),且在区间(0,+∞)上单调递增,若实数a满足2f(log2a)+f(log
a)≤f(1),则a的取值范围是( )
| 1 |
| 2 |
| A、[1,2] | ||
B、(0,
| ||
| C、(0,2] | ||
| D、(-∞,2] |
若{an}是等差数列,首项a1>0,a1007+a1008>0,a1007•a1008<0,则使前n项和Sn>0成立的最大自然数n是( )
| A、2012 | B、2013 |
| C、2014 | D、2015 |
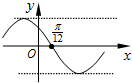 若函数f(x)=sin(ωx+φ)-cos(ωx+φ) (ω>0,0<φ<2π),满足f(x+
若函数f(x)=sin(ωx+φ)-cos(ωx+φ) (ω>0,0<φ<2π),满足f(x+