题目内容
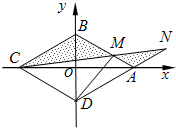 如图,菱形ABCD的边长为2,∠BAD=60°,M为AB边上不与端点重合的动点,且CM与DA分别延长后交于点N,若以菱形的对角线所在直线为坐标轴建立平面直角坐标系,并设BM=2t (0<t<1).
如图,菱形ABCD的边长为2,∠BAD=60°,M为AB边上不与端点重合的动点,且CM与DA分别延长后交于点N,若以菱形的对角线所在直线为坐标轴建立平面直角坐标系,并设BM=2t (0<t<1).(Ⅰ)试用t表示
| DM |
| BN |
(Ⅱ)设f(t)=
| DM |
| BN |
①存在t1,t2∈(0,1),使得
| 2 |
| f(t1) |
②对任意t1∈(0,1),恒存在t2∈(0,1),使得
| 2 |
| f(t1) |
考点:函数与方程的综合运用
专题:函数的性质及应用,平面向量及应用
分析:(I)过点M作坐标轴的垂线段,由菱形ABCD的边长为2,∠BAD=60°,M为AB边上不与端点重合的动点,BM=2t,可得M点的坐标,进而可得向量
的坐标,由△BCM∽△ANM,可得AN的长,进而得到N点坐标,可得向量
的坐标,结合向量夹角公式,可得他们的夹角;
(II)由(I)可得f(t)的解析式,分别求出两个函数的值域A,B;
①若存在t1,t2∈(0,1),使得
=g(t2) 成立,则只要两函数的值域A=(0,1)与B=(4-2a,4-a)存在公共元素即可,
②对任意t1∈(0,1),恒存在t2∈(0,1),使得
=g(t2)成立,则t∈(0,1)时,函数y=g(t)必取遍函数y=
值域A=(0,1)中的所有值,此即A⊆B.
| DM |
| BN |
(II)由(I)可得f(t)的解析式,分别求出两个函数的值域A,B;
①若存在t1,t2∈(0,1),使得
| 2 |
| f(t1) |
②对任意t1∈(0,1),恒存在t2∈(0,1),使得
| 2 |
| f(t1) |
| 2 |
| f(t) |
解答:
 解:( I ) 过点M作坐标轴的垂线段,
解:( I ) 过点M作坐标轴的垂线段,
则依题设易求得M点的坐标为:M(
t,1-t ),即
=(
t,1-t ),…(1)
依题设知:△ABD为正三角形,故
=(0,-1),
由此知:
=
-
=(
t,2-t ),…(2)
又依题设知:△BCM∽△ANM,
∴
=
=
=
,
∴AN=2(
),
又∵∠NAx=30°,
∴yN=AN•sin30°=
,且xN=
+AN•cos30°=
,
由此可得:
=(
,
),
又
=(0,1),
∴
=
-
=(
,
)…(3)
由(2),(3)两式得:
•
=2(
),且|
||
|=4(
).
故cos<
,
>=
,
又<
,
>∈[0,π],
∴<
,
>=60°为所求.
( II )由( I )知:f(t)=2(t+
-1),且由0<t<1知:f(t)>2,
∴函数y=
的值域为A=(0,1).
另由a>0知:函数y=g(t),t1∈(0,1)的值域为:B=(4-2a,4-a).
①若存在t1,t2∈(0,1),使得
=g(t2) 成立,则只要两函数的值域A=(0,1)与B=(4-2a,4-a)存在公共元素即可.此时A与B间的关系有以下三种可能:
( i ) A⊆B时,则必
⇒2≤a≤3;
( ii ) A∩B≠∅时,则0<4-2a<1,或0<4-a<1,⇒
<a<2,或3<a<4;
(iii) B⊆A时,则必
⇒a无解. 综上,
<a<4,为所求.
②对任意t1∈(0,1),恒存在t2∈(0,1),使得
=g(t2)成立,则t∈(0,1)时,函数y=g(t)必取遍函数y=
值域A=(0,1)中的所有值,此即A⊆B,故由①知:2≤a≤3为所求.
 解:( I ) 过点M作坐标轴的垂线段,
解:( I ) 过点M作坐标轴的垂线段,则依题设易求得M点的坐标为:M(
| 3 |
| OM |
| 3 |
依题设知:△ABD为正三角形,故
| OD |
由此知:
| DM |
| OM |
| OD |
| 3 |
又依题设知:△BCM∽△ANM,
∴
| AN |
| BC |
| AM |
| BM |
| 2-2t |
| 2t |
| 1-t |
| t |
∴AN=2(
| 1-t |
| t |
又∵∠NAx=30°,
∴yN=AN•sin30°=
| 1-t |
| t |
| 3 |
| ||
| t |
由此可得:
| ON |
| ||
| t |
| 1-t |
| t |
又
| OB |
∴
| BN |
| ON |
| OB |
| ||
| t |
| 1-2t |
| t |
由(2),(3)两式得:
| DM |
| BN |
| t2-t+1 |
| t |
| DM |
| BN |
| t2-t+1 |
| t |
故cos<
| DM |
| BN |
| 1 |
| 2 |
又<
| DM |
| BN |
∴<
| DM |
| BN |
( II )由( I )知:f(t)=2(t+
| 1 |
| t |
∴函数y=
| 2 |
| f(t) |
另由a>0知:函数y=g(t),t1∈(0,1)的值域为:B=(4-2a,4-a).
①若存在t1,t2∈(0,1),使得
| 2 |
| f(t1) |
( i ) A⊆B时,则必
|
( ii ) A∩B≠∅时,则0<4-2a<1,或0<4-a<1,⇒
| 3 |
| 2 |
(iii) B⊆A时,则必
|
| 3 |
| 2 |
②对任意t1∈(0,1),恒存在t2∈(0,1),使得
| 2 |
| f(t1) |
| 2 |
| f(t) |
点评:本题考查的知识点是函数的图象和性质,平面向量共线,夹角,数量积,是函数和向量的综合应用,综合性强,运算量大,转化困难,属于难题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
已知-1,x,-4成等比数列,则x的值为( )
| A、2 | ||||
B、-
| ||||
| C、2 或-2 | ||||
D、-
|
已知sinx+siny=
,则u=sinx+cos2x的最小值是( )
| 1 |
| 3 |
A、-
| ||
| B、-1 | ||
| C、1 | ||
D、
|
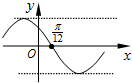 若函数f(x)=sin(ωx+φ)-cos(ωx+φ) (ω>0,0<φ<2π),满足f(x+
若函数f(x)=sin(ωx+φ)-cos(ωx+φ) (ω>0,0<φ<2π),满足f(x+