题目内容
在数列{an}中,a1=-
,an=1-
(n>1),则a2014的值为( )
| 1 |
| 4 |
| 1 |
| an-1 |
A、-
| ||
| B、5 | ||
C、
| ||
| D、以上都不对 |
考点:数列的函数特性
专题:等差数列与等比数列
分析:利用递推公式推导出数列{an}是周期为3的周期数列,由此能求出结果.
解答:
解:在数列{an}中,a1=-
,an=1-
(n>1),
∴a2=1-
=5,
a3=1-
=
,
a4=1-
=-
,
∴数列{an}是周期为3的周期数列,
∵2014=671×3+1,
∴a2014=a1=-
.
故选:A.
| 1 |
| 4 |
| 1 |
| an-1 |
∴a2=1-
| 1 | ||
-
|
a3=1-
| 1 |
| 5 |
| 4 |
| 5 |
a4=1-
| 1 | ||
|
| 1 |
| 4 |
∴数列{an}是周期为3的周期数列,
∵2014=671×3+1,
∴a2014=a1=-
| 1 |
| 4 |
故选:A.
点评:本题考查数列的第2014项的求法,是基础题,解题时要认真审题上,注意递推思想的合理运用.

练习册系列答案
相关题目
已知-1,x,-4成等比数列,则x的值为( )
| A、2 | ||||
B、-
| ||||
| C、2 或-2 | ||||
D、-
|
若{an}是等差数列,首项a1>0,a1007+a1008>0,a1007•a1008<0,则使前n项和Sn>0成立的最大自然数n是( )
| A、2012 | B、2013 |
| C、2014 | D、2015 |
已知m=a+
(a>2),n=2 2-b2(b≠0),则m,m的大小关系是( )
| 1 |
| a-2 |
| A、m>n | B、m<n |
| C、m=n | D、不确定 |
已知双曲线
-
=1的实轴长、虚轴长、焦距依次成等比数列,则其离心率为( )
| x2 |
| a2 |
| y2 |
| b2 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
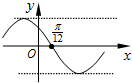 若函数f(x)=sin(ωx+φ)-cos(ωx+φ) (ω>0,0<φ<2π),满足f(x+
若函数f(x)=sin(ωx+φ)-cos(ωx+φ) (ω>0,0<φ<2π),满足f(x+