Question

过点P（1，

2

）的直线l将圆（x-2）²+y²=4分成两段弧，当劣弧所对的圆心角最小时，直线l的斜率k等于（　　）

• A、-

  2

  2

• B、

  2

  2

• C、-

  1

  2

• D、

  1

  2

Answer 1

考点：直线与圆相交的性质

专题：计算题,直线与圆

分析：先要画出满足条件的图形，数形结合容易得到符合题目中的条件的数理关系，由劣弧所对的圆心角最小弦长最短，及过圆内一点最短的弦与过该点的直径垂直，易得到解题思路．

解答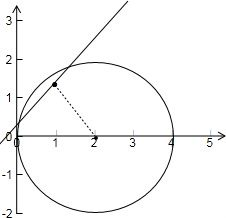： 解：如图示，由图形可知：
点P（1，

2

）在圆（x-2）²+y²=4的内部，
圆心为O（2，0）要使得劣弧所对的圆心角最小，
只能是直线l⊥OA，
所以k_l=-

1

kOA

=-

1

- 2

=

2

2

．
故选：B．

点评：垂径定理及其推论是解决直线与圆关系时常用的定理，要求大家熟练掌握，垂径定理：垂直于弦的直径平分这条弦，并且平分这条弦所对的两条弧．相关推论，过圆内一点垂直于该点直径的弦最短，且弦所在的劣弧最短，优弧最长，弦所对的圆心角、圆周角最小．