题目内容
已知函数f（x）=
，若a，b，c是互不相等的实数，且满足f（a）=f（b）=f（c），则abc的取值范围是 ．
|
考点：分段函数的应用
专题：计算题,数形结合,函数的性质及应用
分析：图解法：画出函数f（x）=
的图象，根据图象分析abc的取值范围．
|
解答：
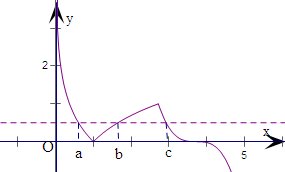解：如图，画出f（x）=
的图象，
设a＜b＜c，则|lna|=|lnb|，
即有lna+lnb=0，即有ab=1，
当x＞e时，y=-（x-e-1）3递减，
且与x轴交于（e+1，0），
∴abc=c，且e＜c＜e+1，
可得abc的取值范围是（e，e+1）．
故答案为：（e，e+1）．
解：如图，画出f（x）=
|
的图象，
设a＜b＜c，则|lna|=|lnb|，
即有lna+lnb=0，即有ab=1，
当x＞e时，y=-（x-e-1）3递减，
且与x轴交于（e+1，0），
∴abc=c，且e＜c＜e+1，
可得abc的取值范围是（e，e+1）．
故答案为：（e，e+1）．
点评：此题是个中档题．考查利用函数图象分析解决问题的能力，以及对数函数图象的特点，体现数形结合的思想．
练习册系列答案
名师点拨卷系列答案
相关题目
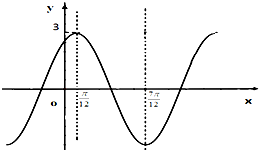已知函数f（x）=Asin（wx+φ）（w＞0，A＞0，|φ|＜
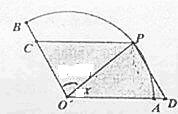半径为1，圆心角为120°的扇形，点P是扇形AB弧上的动点，设∠POA=x．