题目内容
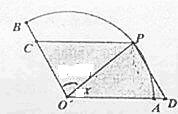半径为1，圆心角为120°的扇形，点P是扇形AB弧上的动点，设∠POA=x．（1）用x表示平行四边形ODPC的面积S=f（x）；
（2）求平行四边形ODPC面积的最大值．
考点：扇形面积公式
专题：计算题,三角函数的求值
分析：（1）利用正弦定理求出PC，OC，即可用x表示平行四边形ODPC的面积S=f（x）；
（2）利用辅助角公式化简，即可求平行四边形ODPC面积的最大值．
（2）利用辅助角公式化简，即可求平行四边形ODPC面积的最大值．
解答：
解：（1）由题意得：
=
=
，
∴PC=
sin(120°-x)，OC=
sinx
∴S=
sin（120°-x）sinx，x∈（0°，120°）；
（2）S=
（
cosx+
sinx）sinx=
[sin（2x-30°）+
]
当2x-30°=90°时达最大值，
即当x=60°时．平行四边形面积达到最大值
．
| PC |
| sin(120°-x) |
| 1 |
| sin60° |
| OC |
| sinx |
∴PC=
| 2 | ||
|
| 2 | ||
|
∴S=
| 4 |
| 3 |
（2）S=
| 4 |
| 3 |
| ||
| 2 |
| 1 |
| 2 |
| 2 |
| 3 |
| 1 |
| 2 |
当2x-30°=90°时达最大值，
即当x=60°时．平行四边形面积达到最大值
| ||
| 2 |
点评：本题考查正弦定理，考查辅助角公式的运用，考查学生分析解决问题的能力，属于中档题．
练习册系列答案
暑假作业海燕出版社系列答案
相关题目
下列函数中，为奇函数的是（ ）
| A、f（x）=x-1 |
| B、f（x）=x |
| C、f（x）=-3x+2 |
| D、f（x）=2x2 |
2014年我国公布了新的高考改革方案，在招生录取制度改革方面，普通高校逐步推行基于统一高考和高中学业水平考试成绩的综合评价、多元录取机制，普通高校招生录取将参考考生的高中学业水平考试成绩和职业倾向性测试成绩．为了解公众对“改革方案”的态度，随机抽查了50人，将调查情况进行整理后制成下表：