题目内容
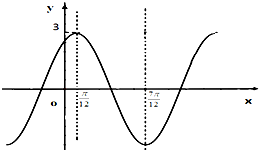已知函数f（x）=Asin（wx+φ）（w＞0，A＞0，|φ|＜| π |
| 2 |
（1）求f（x）的解析式；
（2）若f（
| θ |
| 2 |
| π |
| 6 |
| 12 |
| 5 |
| π |
| 2 |
| π |
| 3 |
考点：正弦函数的图象
专题：函数的性质及应用
分析：（1）由函数的图象的顶点坐标求出A，由周期求出ω，由图象经过特殊点求出φ的值，可得函数的解析式．
（2）由f（
-
）的值求得 sinθ 的值，根据可得cosθ 的值，从而求得cos（θ-
）=cosθcos
+sinθsin
的值．
（2）由f（
| θ |
| 2 |
| π |
| 6 |
| π |
| 3 |
| π |
| 3 |
| π |
| 3 |
解答：
解：（1）由图可知，A=3，
T=
=
-
，∴ω=2，f（x）=3sin（2x+φ）．
而函数f（x）图象经过点（
，3），∴3sin（2×
x+φ）=3，∴
+φ=2kπ+
，k∈z，
即 φ=2kπ+
，k∈z．
结合，|φ|＜
，可得φ=
，f（x）=3sin（2x+
）．
（2）∵f（
-
）=3sinθ=
，∴sinθ=
．
根据θ∈（0，
），可得cosθ=
，∴cos（θ-
）=cosθcos
+sinθsin
=
×
+
×
=
．
| 1 |
| 2 |
| π |
| ω |
| 7π |
| 12 |
| π |
| 12 |
而函数f（x）图象经过点（
| π |
| 12 |
| π |
| 12 |
| π |
| 6 |
| π |
| 2 |
即 φ=2kπ+
| π |
| 3 |
结合，|φ|＜
| π |
| 2 |
| π |
| 3 |
| π |
| 3 |
（2）∵f（
| θ |
| 2 |
| π |
| 6 |
| 12 |
| 5 |
| 4 |
| 5 |
根据θ∈（0，
| π |
| 2 |
| 3 |
| 5 |
| π |
| 3 |
| π |
| 3 |
| π |
| 3 |
| 3 |
| 5 |
| 1 |
| 2 |
| 4 |
| 5 |
| ||
| 2 |
3+4
| ||
| 10 |
点评：本题主要考查由函数y=Asin（ωx+φ）的部分图象求解析式，同角三角函数的基本关系，两角差的余弦公式的应用，属于中档题．
练习册系列答案
阅读快车系列答案
相关题目
已知四面体P-ABC的四个顶点都在球O的球面上，若PB⊥平面ABC，AB⊥AC，且AC=1，PB=AB=2，则球O的体积为（ ）
A、
| ||
B、
| ||
| C、4π | ||
D、
|
下列不等式中成立的是（ ）
| A、tan1＞sin1＞cos1 |
| B、tan1＞cos1＞sin1 |
| C、cos1＞sin1＞tan1 |
| D、sin1＞tan1＞cos1 |