题目内容
设变量x，y满足约束条件
，则目标函数z=-x-y的取值范围是（ ）
|
| A、[-4，0] |
| B、[-8，-2] |
| C、[-4，-2] |
| D、[-4，-1] |
考点：简单线性规划
专题：数形结合,不等式的解法及应用
分析：作出不等式组对应的平面区域，利用z的几何意义，利用数形结合，即可得到结论．
解答：
解：作出不等式组对应的平面区域如图：
由z=-x-y得y=-x-z，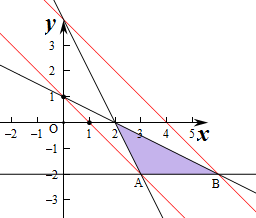
平移直线y=-x-z，由图象可知当直线y=-x-z经过点B时，
直线的截距最大，此时z最小．
经过点A时，直线的截距最小，此时z最大．
由
，解得
，
即B（6，-2），此时zmin=-6-（-2）=-4，
由
，解得
，
即A（3，-2），此时zmax=-3-（-2）=-1，
即-4≤z≤-1，
故选：D．
由z=-x-y得y=-x-z，
平移直线y=-x-z，由图象可知当直线y=-x-z经过点B时，
直线的截距最大，此时z最小．
经过点A时，直线的截距最小，此时z最大．
由
|
|
即B（6，-2），此时zmin=-6-（-2）=-4，
由
|
|
即A（3，-2），此时zmax=-3-（-2）=-1，
即-4≤z≤-1，
故选：D．
点评：本题主要考查线性规划的应用，利用数形结合是解决本题的关键．
练习册系列答案
相关题目
在盒子中装有2个白球和2个红球，每次从中随机取出一个球，第三次恰好将白球取完的概率为（ ）
A、
| ||
B、
| ||
C、
| ||
D、
|
已知变量x，y满足
，则xy的最大值为（ ）
|
| A、1 | B、2 | C、3 | D、4 |
已知函数f(x)=x+
，则函数y=f（x）的大致图象为（ ）
| ln|x| |
| x |
A、 |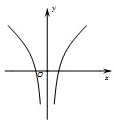
B、 |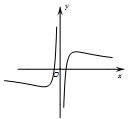
C、 |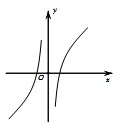
D、 |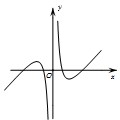
下列命题中，真命题是（ ）
| A、存在一个△ABC，使a2=b2+c2-3bccosA（a，b，c是三边长，a是内角A的对边） |
| B、?x∈（1，+∞），log0.5x＞0 |
| C、幂函数 f（x）=（m-1）xm-3在定义域上是减函数 |
| D、a＞1，b＞1是ab＞1的必要条件 |
若实数x，y满足
，则z=3x+2y的最大值是（ ）
|
| A、0 | ||
| B、1 | ||
C、
| ||
| D、9 |