题目内容
已知函数f(x)=x+
,则函数y=f(x)的大致图象为( )
| ln|x| |
| x |
A、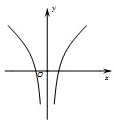 |
B、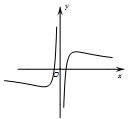 |
C、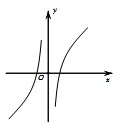 |
D、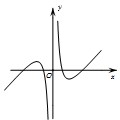 |
考点:利用导数研究函数的单调性,函数的图象,对数函数的图像与性质
专题:计算题,作图题,导数的综合应用
分析:可得函数为奇函数,进而求导数可得(0,+∞)上的单调性,结合选项分析可得答案.
解答:
解:由题意可得函数的定义域为(-∞,0)∪(0,+∞),
f(x)=x+
,可得f(-x)=-f(x),
故函数为奇函数,其图象关于原点对称,且在对称区间的单调性一致,
故只需研究当x>0时的单调性即可,
当x>0时,f′(x)=1+
=
,
令g(x)=x2+1-lnx,(x>0),
g′(x)=2x-
=
,
令g′(x)=0,解得x=
,
故当0<x<
时,g′(x)<0,g(x)是减函数,
x>
时,函数g(x)是单调递增,g(x)的最小值为g(
)=
+1-ln
>0,
∴f′(x)>0在x>0时,恒成立,函数是单调增函数,
综上可得选项C符合题意,
故选:C.
f(x)=x+
| ln|x| |
| x |
故函数为奇函数,其图象关于原点对称,且在对称区间的单调性一致,
故只需研究当x>0时的单调性即可,
当x>0时,f′(x)=1+
| 1-lnx |
| x2 |
| x2+1-lnx |
| x2 |
令g(x)=x2+1-lnx,(x>0),
g′(x)=2x-
| 1 |
| x |
| 2x2-1 |
| x |
令g′(x)=0,解得x=
| ||
| 2 |
故当0<x<
| ||
| 2 |
x>
| ||
| 2 |
| ||
| 2 |
| 1 |
| 2 |
| ||
| 2 |
∴f′(x)>0在x>0时,恒成立,函数是单调增函数,
综上可得选项C符合题意,
故选:C.
点评:本题考查函数的性质、导数,考查函数的图象,由函数的性质入手是解决问题的关键,属中档题.

练习册系列答案
相关题目
如果一个空间几何体的正视图、侧视图、俯视图都是半径等于5的圆,那么这个空间几何体的表面积等于( )
| A、100π | ||
B、
| ||
| C、25π | ||
D、
|
设变量x,y满足约束条件
,则目标函数z=-x-y的取值范围是( )
|
| A、[-4,0] |
| B、[-8,-2] |
| C、[-4,-2] |
| D、[-4,-1] |
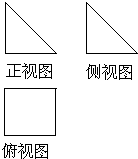 一几何体的三视图如图所示,若正视图和侧视图都是等腰直角三角形,直角边长为1,则该几何体外接球的表面积为( )
一几何体的三视图如图所示,若正视图和侧视图都是等腰直角三角形,直角边长为1,则该几何体外接球的表面积为( )A、
| ||
| B、2π | ||
| C、3π | ||
| D、12π |
给出下列语句:
①二次函数是偶函数吗?
②2>2;
③sin
=1;
④x2-4x+4=0.
其中是命题的有( )
①二次函数是偶函数吗?
②2>2;
③sin
| π |
| 2 |
④x2-4x+4=0.
其中是命题的有( )
| A、1个 | B、2个 | C、3个 | D、4个 |
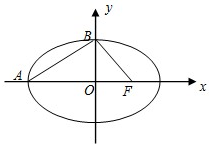 已知椭圆C:
已知椭圆C: