Question

下列结论正确的是

 

（写出正确结论的序号）
①直线l：（2m+1）x+（m+1）y=7m+4，无论m为何值时，l恒过定点（3，1）
②若a₁，a₂，…，a₂₀这20个数据的平均数为

.

x

，方差为0.20，则a₁，a₂，…，a₂₀，

.

x

这21个数据的方差为0.2．
③某同学使用计算器求30个数据的平均数时，错将其中一个数据105输入为15，那么由此求出的平均数与实际平均数的差为-3．
④过直线l₁：x+2=0与l₂：4x+3y+5=0的交点，且与点A（-1，-2）的距离等于1的直线l的方程为3x+y+5=0．
⑤若直线y=x+k和半圆y=

1-x2

只有一个交点，则k的取值范围为-1≤k＜1．

Answer 1

考点：命题的真假判断与应用

专题：简易逻辑

分析：①直线l：（2m+1）x+（m+1）y=7m+4，化为m（2x+y-7）+（x+y-4）=0，联立

2x+y-7=0 x+y-4=0

，解得即可得出；
②若a₁，a₂，…，a₂₀这20个数据的平均数为

.

x

，方差为0.20，则a₁，a₂，…，a₂₀，

.

x

这21个数据的平均数=

20 . x + . x

21

=

.

x

，没有改变，因此方差变为

1

21

(20×0.2+0)．
③某同学使用计算器求30个数据的平均数时，错将其中一个数据105输入为15，那么由此求出的平均数=

29 i=1 xi+15

30

，实际平均数=

29 i=1 +105

30

，即可判断出；
④联立

x+2=0 4x+3y+5=0

，解得

x=-2 y=1

，即（-2，1），分类讨论：当直线l的斜率存在时，设方程为y-1=k（x+2），由点A（-1，-2）的距离等于1，可得

|-k+2+2k+1|

1+k2

=1，解得k；当直线l的斜率不存在时，直线l的方程为x=-2，即可判断出．
⑤若直线y=x+k和半圆y=

1-x2

只有一个交点，如图所示，当-1≤k＜1．时，直线与半圆只有一个交点；当直线与半圆相切时，k=

2

．即可判断出．

解答： 解：①直线l：（2m+1）x+（m+1）y=7m+4，化为m（2x+y-7）+（x+y-4）=0，联立

2x+y-7=0 x+y-4=0

，解得

x=3 y=1

，
因此无论m为何值时，l恒过定点（3，1），正确；
②若a₁，a₂，…，a₂₀这20个数据的平均数为

.

x

，方差为0.20，则a₁，a₂，…，a₂₀，

.

x

这21个数据的平均数=

20 . x + . x

21

=

.

x

，没有改变，因此方差变为

1

21

(20×0.2+0)=

20

21

×0.2，因此不正确．
③某同学使用计算器求30个数据的平均数时，错将其中一个数据105输入为15，那么由此求出的平均数=

29 i=1 xi+15

30

，
实际平均数=

29 i=1 +105

30

，其差=

15-105

30

=-3，正确．
④直线l₁：x+2=0与l₂：4x+3y+5=0的交点，满足

x+2=0 4x+3y+5=0

，解得

x=-2 y=1

，即（-2，1），当直线l的斜率存在时，设方程为y-1=k（x+2），由点A（-1，-2）的距离等于1，可得

|-k+2+2k+1|

1+k2

=1，解得k=-

4

3

．化为4x+3y+5=0；当直线l的斜率不存在时，直线l的方程为x=-2，因此③不正确．
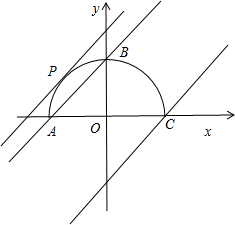
⑤若直线y=x+k和半圆y=

1-x2

只有一个交点，如图所示，当-1≤k＜1．时，直线与半圆只有一个交点；当直线与半圆相切时，k=

2

．因此k的取值范围为
-1≤k＜1或k=

2

，故不正确．
综上可得：只有①③正确．
故答案为：①③．

点评：本题综合考查了简易逻辑的判定、直线系的应用、平均数与方差的计算、点到直线的距离公式、直线与圆的位置关系，考查了推理能力与计算能力，考查了数形结合的思想方法，属于难题．