题目内容

直线mx+
3
ay-m=0（m≠0）过点（0，1），则它的倾斜角为（　　）
A、30°B、45°
C、120°D、135°
考点：直线的倾斜角
专题：直线与圆
分析：利用直线经过的点，求出a，m的关系，求出直线的斜率，然后求解倾斜角．
解答： 解：直线mx+
3
ay-m=0（m≠0）过点（0，1），
所以m=
3
a．
直线的斜率为：-
m
3
a
=-1．
直线的倾斜角为：α，所以tanα=-1，α=135°．
故选：D．
点评：本题考查直线的斜率与直线的倾斜角的关系，点与直线的位置关系，基本知识的考查．
练习册系列答案
相关题目
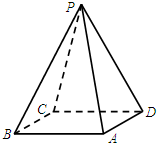点P为正方形ABCD所在平面外一点，AD=3，PD=2
3
，PD⊥AD，若二面角P-AD-C的大小是60°，则二面角P-AB-C的大小是（　　）
A、30°B、45°
C、60°D、90°
从集合{0，1，2，3，4}中随机取出两个不同的数字分别作为点P的横坐标和纵坐标，已知圆C：x2+y2=12．
（1）求点P在圆C内的概率；
（2）若过在圆C内的点P的直线l与圆C分别交于点M，N，当原点到直线l的距离最大时，在圆C内随机撒一粒豆子，求豆子落在△MON（O为原点）内的概率．
△ABC内接于以O为圆心半径为1的圆，且3
OA
+4
OB
+5
OC
=
0
，则S△AOB=
 
．
若函数f（x）=-x2+mx+1在区间[-2，1]上的最大值就是函数f（x）的极大值，则m的取值范围是
 
．
长沙市对地铁1、2号线计价“起步价2元可乘6公里采用“递远递减”的计价原则”进行调查，随机抽查了50人，他们月收入的频数分布及对“计价方案”赞成人数如下表．
月收入（单位：百元）[15，25）[25，35）[35，45）[45，55）[55，65）[65，75）
频数510151055
赞成人数4815521
（1）由以上统计数据填写下面2乘2列联表并问是否有99%的把握认为月收入以5500为分界点对“计价方案”的态度有差异：
 月收入不低于55百元的人数月收入低于55百元的人数合计
赞成a=c= 
不赞成b=d= 
合计   
（2）若对月收入在[15，25），[25，35）的被调查人中各随机选取两人进行追踪调查，记选中的四个人中不赞成“计价方案”的人数为ξ，求随机变量ξ的分布列及数学期望．
参考数据：
P（K2≥k）0.0500.0100.001
k3.8416.63510.828
K2=
n(ad-bc)2
(a+b)(c+d)(a+c)(b+d)
．
下列结论正确的是
 
（写出正确结论的序号）
①直线l：（2m+1）x+（m+1）y=7m+4，无论m为何值时，l恒过定点（3，1）
②若a1，a2，…，a20这20个数据的平均数为
.
x
，方差为0.20，则a1，a2，…，a20，
.
x
这21个数据的方差为0.2．
③某同学使用计算器求30个数据的平均数时，错将其中一个数据105输入为15，那么由此求出的平均数与实际平均数的差为-3．
④过直线l1：x+2=0与l2：4x+3y+5=0的交点，且与点A（-1，-2）的距离等于1的直线l的方程为3x+y+5=0．
⑤若直线y=x+k和半圆y=
1-x2
只有一个交点，则k的取值范围为-1≤k＜1．
函数f（x）=ax+
b
x-1
-a（a∈R，a≠0）在x=3处的切线方程与直线（2a-1）x-2y+3=0平行且f（3）=3，若方程f（x）=t（x2-2x+3）|x|有三个解，则实数t的取值范围为
 
．
函数f（x）=x2-2x在区间[2，4]上的最小值为（　　）
A、-1B、0C、3D、8

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网