题目内容
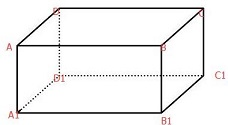 如图,在长方体ABCD-A1B1C1D1中,AB=6,AD=3
如图,在长方体ABCD-A1B1C1D1中,AB=6,AD=3| 2 |
考点:二面角的平面角及求法
专题:空间角
分析:连结BD,作AO⊥BD于O,连结A1O,说明∠A1OA为所求二面角A-BD-A1的平面角.通过tan∠A1OA=
求出角的大小,即可.
| AA1 |
| AO |
解答:
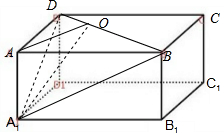 解:连结BD,作AO⊥BD于O,连结A1O,因为几何体是长方体,可知BD⊥平面AOA1,所以∠A1OA为所求二面角A-BD-A1的平面角.
解:连结BD,作AO⊥BD于O,连结A1O,因为几何体是长方体,可知BD⊥平面AOA1,所以∠A1OA为所求二面角A-BD-A1的平面角.
在长方体ABCD-A1B1C1D1中,AB=6,AD=3
,AA1=2,
∴BD=
=3
.AO=
=2
.
∴tan∠A1OA=
=
=
.
∠A1OA=
.
故答案为:
.
 解:连结BD,作AO⊥BD于O,连结A1O,因为几何体是长方体,可知BD⊥平面AOA1,所以∠A1OA为所求二面角A-BD-A1的平面角.
解:连结BD,作AO⊥BD于O,连结A1O,因为几何体是长方体,可知BD⊥平面AOA1,所以∠A1OA为所求二面角A-BD-A1的平面角.在长方体ABCD-A1B1C1D1中,AB=6,AD=3
| 2 |
∴BD=
| AB2+AD2 |
| 6 |
| AB•AD |
| BD |
| 3 |
∴tan∠A1OA=
| AA1 |
| AO |
| 2 | ||
2
|
| ||
| 3 |
∠A1OA=
| π |
| 6 |
故答案为:
| π |
| 6 |
点评:本题考查二面角的平面角的求法,作出二面角的平面角,然后求解是的关键.也可以利用空间向量的数量积求解.

练习册系列答案
相关题目
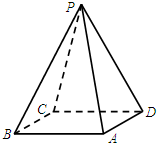 点P为正方形ABCD所在平面外一点,AD=3,PD=2
点P为正方形ABCD所在平面外一点,AD=3,PD=2| 3 |
| A、30° | B、45° |
| C、60° | D、90° |