题目内容
已知关于x的一元二次方程f(x)=ax2-4bx+1
(1)设集合P={1,2,3},Q={-1,1,2,3,4},分别从集合P,Q中随机取一个数为a和b,求函数y=f(x)在[1,+∞)上是增函数的概率
(2)设点(a,b)是区域
内的随机点,设A={f(1)<0},求事件A发生的概率.
(1)设集合P={1,2,3},Q={-1,1,2,3,4},分别从集合P,Q中随机取一个数为a和b,求函数y=f(x)在[1,+∞)上是增函数的概率
(2)设点(a,b)是区域
|
考点:几何概型
专题:概率与统计
分析:(Ⅰ)根据古典概率的概率公式进行计算即可求出概率.
(Ⅱ)根据几何概型的概率公式进行计算即可.
(Ⅱ)根据几何概型的概率公式进行计算即可.
解答:
解(Ⅰ)∵函数f(x)=ax2-4bx+1的图象的对称轴为x=
,
要使f(x)=ax2-4bx+1在区间[1,+∞)上为增函数,
当且仅当a>0且x=
≤1,
即2b≤a.
若a=1,则b=-1;
若a=2,则b=-1,1;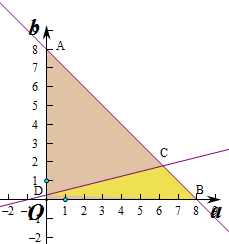
若a=3,则b=-1,1,
∴事件包含基本事件的个数是1+2+2=5
∴所求事件的概率为
=
.
(Ⅱ)由(1)知当且仅当2b≤a.且a>0时,
函数f(x)=ax2-4bx+1在区间[1,+∞)上为增函数,
依条件可知试验的全部结果所构成的区域为{(a,b)|
}
构成所求事件的区域为三角形部分对应的面积S=
×8×8=32.
事件A满足{(a,b)|
}={(a,b)|
},
由
,解得a=
,b=
,即交点坐标(
,
),
则对应三角形的面积S=
×(8-
)×
=
,
则所求事件的概率为P=
=
.
| 2b |
| a |
要使f(x)=ax2-4bx+1在区间[1,+∞)上为增函数,
当且仅当a>0且x=
| 2b |
| a |
即2b≤a.
若a=1,则b=-1;
若a=2,则b=-1,1;

若a=3,则b=-1,1,
∴事件包含基本事件的个数是1+2+2=5
∴所求事件的概率为
| 5 |
| 15 |
| 1 |
| 3 |
(Ⅱ)由(1)知当且仅当2b≤a.且a>0时,
函数f(x)=ax2-4bx+1在区间[1,+∞)上为增函数,
依条件可知试验的全部结果所构成的区域为{(a,b)|
|
构成所求事件的区域为三角形部分对应的面积S=
| 1 |
| 2 |
事件A满足{(a,b)|
|
|
由
|
| 31 |
| 5 |
| 9 |
| 5 |
| 31 |
| 5 |
| 9 |
| 5 |
则对应三角形的面积S=
| 1 |
| 2 |
| 1 |
| 4 |
| 31 |
| 5 |
| 961 |
| 40 |
则所求事件的概率为P=
| ||
| 32 |
| 961 |
| 1280 |
点评:本题只要考查概率的求法,要求熟练掌握古典概型和几何概型的概率公式,注意它们之间的联系和区别.

练习册系列答案
相关题目
函数f(x)=ax+
-a(a∈R,a≠0)在x=3处的切线方程与直线(2a-1)x-2y+3=0平行且f(3)=3,若方程f(x)=t(x2-2x+3)|x|有三个解,则实数t的取值范围为 .
| b |
| x-1 |
已知点D为等腰直角三角形ABC斜边AB的中点,则下列等式中不恒成立的是( )
A、
| ||||||||||||||
B、
| ||||||||||||||
C、
| ||||||||||||||
D、(
|
在可行域内任取一点,规则为如图所示的流程图,则能输出数对(s,t)的概率是( )


A、
| ||
B、
| ||
C、
| ||
D、
|