题目内容
已知向量
=（
，1），向量
=（sin2x，cos2x），函数f（x）=
•
．
（1）求函数f（x）的表达式，并作出函数y=f（x）在一个周期内的简图（用五点法列表描点）；
（2）求函数y=f（x）的周期，并写单调区间．
| a |
| 3 |
| b |
| a |
| b |
（1）求函数f（x）的表达式，并作出函数y=f（x）在一个周期内的简图（用五点法列表描点）；
（2）求函数y=f（x）的周期，并写单调区间．
考点：平面向量数量积的运算,三角函数中的恒等变换应用
专题：计算题,三角函数的图像与性质,平面向量及应用
分析：（1）由平面向量的数量积公式和两角和的正弦公式，即可得到f（x）=
sin2x+cos2x=2sin（2x+
），运用五点法，即可得到在一个周期内的简图；
（2）由周期公式得到周期；由正弦函数的单调区间，即可得到f（x）的单调区间．
| 3 |
| π |
| 6 |
（2）由周期公式得到周期；由正弦函数的单调区间，即可得到f（x）的单调区间．
解答：
解：（1）由于向量
=（
，1），向量
=（sin2x，cos2x），函数f（x）=
•
．
则有f（x）=
sin2x+cos2x=2sin（2x+
），
函数的周期为T=
=π，先用“五点法”作出一个周期的图象，列表：
描点得整个图象，如右．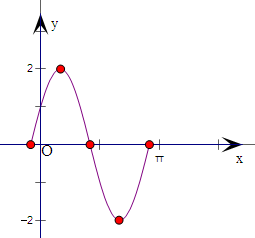
（2）函数y=f（x）的周期为π，
由2kπ-
≤2x+
≤2kπ+
，解得kπ-
≤x≤kπ+
；
由2kπ+
≤2x+
≤2kπ+
，解得kπ+
≤x≤
kπ+
，
则单调增区间[kπ-
，kπ+
]（k为整数）；
单调减区间[kπ+
，kπ+
]（k为整数）．
| a |
| 3 |
| b |
| a |
| b |
则有f（x）=
| 3 |
| π |
| 6 |
函数的周期为T=
| 2π |
| 2 |
| x | -
|
|
|
|
| ||||||||||
2x+
| 0 |
| π |
| 2π | ||||||||||
2sin（2x+
| 0 | 2 | 0 | -2 | 0 |
（2）函数y=f（x）的周期为π，
由2kπ-
| π |
| 2 |
| π |
| 6 |
| π |
| 2 |
| π |
| 3 |
| π |
| 6 |
由2kπ+
| π |
| 2 |
| π |
| 6 |
| 3π |
| 2 |
| π |
| 6 |
kπ+
| 3π |
| 4 |
则单调增区间[kπ-
| π |
| 3 |
| π |
| 6 |
单调减区间[kπ+
| π |
| 6 |
| 3π |
| 4 |
点评：本题考查三角函数的图象和性质，考查三角函数的周期性和单调性，同时考查平面向量的数量积的坐标公式，考查运算能力，属于中档题．
练习册系列答案
智能训练练测考系列答案
相关题目
如图是调查某地某公司1000名员工的月收入后制作的直方图．
某动物园要围建一个面积为360m2的矩形场地，要求矩形场地的一面利用旧墙（利用旧墙需维修），其它三面围墙要新建，在旧墙的对面的新墙上要留一个宽度为2m的进出口，如图所示，已知旧墙的维修费用为45元/m，新墙的造价为180元/m，设利用的旧墙的长度为x（单位：元）．