题目内容
已知函数f(x)=
是R上的增函数,则a的取值范围是 .
|
考点:函数单调性的性质
专题:函数的性质及应用
分析:由条件利用函数的单调性的性质,可得1-2a>1,且 a<0,由此求得a的取值范围.
解答:
解:由于函数f(x)=
是R上的增函数,∴1-2a>1,且a<0,
求得a<0,
故答案为:(-∞,0).
|
求得a<0,
故答案为:(-∞,0).
点评:本题主要考查函数的单调性的性质,属于基础题.

练习册系列答案
相关题目
“f(x)是奇函数”是“f(0)=0”的( )
| A、充分而不必要条件 |
| B、必要而不充分条件 |
| C、充分必要条件 |
| D、既不充分也不必要条件 |
集合M={-2,0,1,2},N={x|x2-x>0},则M∩N=( )
| A、{-2,1,2} |
| B、{0,2} |
| C、{-2,2} |
| D、[-2,2] |
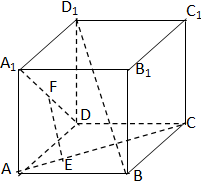
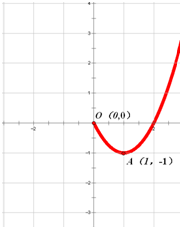 已知f(x)是定义在R上的奇函数,如图为函数f(x)的部分图象.
已知f(x)是定义在R上的奇函数,如图为函数f(x)的部分图象.