题目内容
集合M={-2,0,1,2},N={x|x2-x>0},则M∩N=( )
| A、{-2,1,2} |
| B、{0,2} |
| C、{-2,2} |
| D、[-2,2] |
考点:交集及其运算
专题:集合
分析:求解一元二次不等式化简集合N,然后直接利用交集运算求解.
解答:
解:∵M={-2,0,1,2},
N={x|x2-x>0}={x|x<0或x>1},
则M∩N={-2,0,1,2}∩{x|x<0或x>1}={-2,2}.
故选:C.
N={x|x2-x>0}={x|x<0或x>1},
则M∩N={-2,0,1,2}∩{x|x<0或x>1}={-2,2}.
故选:C.
点评:本题考查了交集及其运算,考查了一元二次不等式的解法,是基础题.

练习册系列答案
 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案
相关题目
下列关系中正确的是( )
A、log76<ln
| ||
B、log3π<ln
| ||
C、ln
| ||
D、ln
|
已知函数f(x)=
+
的定义域是( )
| 1+x |
| x |
| 1-x |
| A、[-1,+∞) |
| B、(-∞,-1] |
| C、[-1,1)∪(1,+∞) |
| D、R |
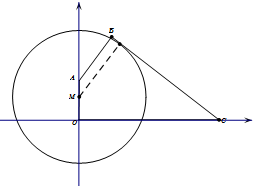 已知四边形OABC中,OA⊥OC,AB⊥BC,且OA=6,OC=17,tan∠BCO=
已知四边形OABC中,OA⊥OC,AB⊥BC,且OA=6,OC=17,tan∠BCO= 三棱柱ABC-A1B1C1中,侧棱与底面垂直,∠ABC=90°,AB=BC=BB1=2,M,N分别是AB,A1C的中点.
三棱柱ABC-A1B1C1中,侧棱与底面垂直,∠ABC=90°,AB=BC=BB1=2,M,N分别是AB,A1C的中点.