题目内容
若点P(-1,5),Q(5,3),过线段PQ的中点,使P,Q两点到直线m的距离都等于3,则直线m的方程是 .
考点:点到直线的距离公式,直线的一般式方程
专题:直线与圆
分析:由已知得线段PQ的中点为(2,4),当直线m的斜率存在时设直线m的方程为kx-y-2k+4=0,当直线m的斜率不存在时,直线m的方程为x=2,由此利用点到直线的距离公式能求出直线m的方程.
解答:
解:∵P(-1,5),Q(5,3),
∴线段PQ的中点为(2,4),
当直线m的斜率存在时设直线m的方程为y-4=k(x-2),即kx-y-2k+4=0,
∵P,Q两点到直线m的距离都等于3,
∴
,
解得k=
,
∴m的方程为
x-y-
+4=0,
整理,得4x-3y+4=0.
当直线m的斜率不存在时,直线m的方程为x=2,满足条件.
∴直线m的方程是x=2或4x-3y+4=0.
故答案为:x=2或4x-3y+4=0.
∴线段PQ的中点为(2,4),
当直线m的斜率存在时设直线m的方程为y-4=k(x-2),即kx-y-2k+4=0,
∵P,Q两点到直线m的距离都等于3,
∴
|
解得k=
| 4 |
| 3 |
∴m的方程为
| 4 |
| 3 |
| 8 |
| 3 |
整理,得4x-3y+4=0.
当直线m的斜率不存在时,直线m的方程为x=2,满足条件.
∴直线m的方程是x=2或4x-3y+4=0.
故答案为:x=2或4x-3y+4=0.
点评:本题考查直线方程的求法,是基础题,解题时要认真审题,注意点到直线的距离公式的合理运用.

练习册系列答案
 百年学典课时学练测系列答案
百年学典课时学练测系列答案 仁爱英语同步练习册系列答案
仁爱英语同步练习册系列答案
相关题目
不等式|4-3x|-5≤0的解集是( )
A、{x|-
| ||
B、{x|x≤-
| ||
C、{x|
| ||
D、{x|-
|
直线λx+y+λ-2=0不过第三象限,则λ的取值范围是( )
| A、[0,1] |
| B、[0,2] |
| C、(-∞,4] |
| D、[4,+∞) |
已知集合A到B的映射f:x→y=
,则集合A中元素3在B中所对应的元素是( )
| 12 |
| x+1 |
| A、1 | B、2 | C、3 | D、4 |
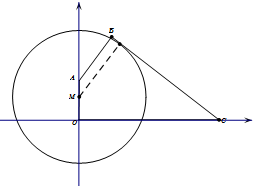 已知四边形OABC中,OA⊥OC,AB⊥BC,且OA=6,OC=17,tan∠BCO=
已知四边形OABC中,OA⊥OC,AB⊥BC,且OA=6,OC=17,tan∠BCO=